 ακέραιοι να αποδείξετε οτι το
ακέραιοι να αποδείξετε οτι το  διαρειται απο το
διαρειται απο το  .
.Συντονιστές: cretanman, silouan, rek2
Δεν είναι δύσκολη απλά θέλει πολλές πράξεις. ΘέτουμεΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Ανακέραιοι να αποδείξετε οτι το
διαρειται απο το
.
 . Αν
. Αν  (αν ο
(αν ο  αποτελεί παράγοντα του
αποτελεί παράγοντα του  ), τότε για
), τότε για  θα πρέπει
θα πρέπει  . Αντικαθιστούμε όπου
. Αντικαθιστούμε όπου  το
το  , εκτελούμε τις πράξεις και παίρνουμε
, εκτελούμε τις πράξεις και παίρνουμε  . Συνεπώς, το ζητούμενο είναι άμεσο.
. Συνεπώς, το ζητούμενο είναι άμεσο.Χάρη εξαρτάτε πως θα το δείςΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Ανακέραιοι να αποδείξετε οτι το
διαρειται απο το
.
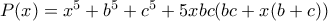

 (1)
(1) πολυώνυμο με ακέραιους συντελεστές.
πολυώνυμο με ακέραιους συντελεστές. οπότε έχουμε μια ωραία ταυτότητα)
οπότε έχουμε μια ωραία ταυτότητα)  στην (1) παίρνουμε το ζητούμενο.
στην (1) παίρνουμε το ζητούμενο.Βασικά θα έπρεπε να μεταφερθεί στην Άλγεβρα (πιστεύω).ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Σας ευχαριστώ για τις λυσεις.
Εντάξει Προχωρημένη NT Juniors το έβαλα. Άλλο αν εχουμε πολλά ταλέντα στοκαι το επίπεδο εχει εκτοξευθεί!
 πολυωνυμική εξίσωση με ρίζες τους
πολυωνυμική εξίσωση με ρίζες τους 
 (1)
(1)

 βρίσκουμε (με μικρή επιφύλαξη για τις πράξεις)
βρίσκουμε (με μικρή επιφύλαξη για τις πράξεις)
 και τελειώσαμε.
και τελειώσαμε.Η ασκηση προέρχεται απο το 111 Problems in ALGEBRA and NUMBER THEORY και βρίσκεται στα προβληματα Number Theory.matha έγραψε:Όπως είπαν και οι προλαλήσαντες δεν είναι δύσκολη, ούτε καν είναι άσκηση θεωρίας αριθμών. Ταιριάζει περισσότερο στα πολυώνυμα. Μια άλλη προσέγγιση είναι η εξής:
Ας είναιπολυωνυμική εξίσωση με ρίζες τους
Τότε
(1)
Προκύπτει
οπότε γράφοντας τις αντίστοιχες για ταβρίσκουμε (με μικρή επιφύλαξη για τις πράξεις)
Εδώ αν γίνουν οι πράξεις, βλέπουμε ότι το πολυώνυμο που προκύπτει έχει παράγοντα τοκαι τελειώσαμε.
Μπορούμε να πάρουμε καιΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Η ασκηση προέρχεται απο το 111 Problems in ALGEBRA and NUMBER THEORY και βρίσκεται στα προβληματα Number Theory.matha έγραψε:Όπως είπαν και οι προλαλήσαντες δεν είναι δύσκολη, ούτε καν είναι άσκηση θεωρίας αριθμών. Ταιριάζει περισσότερο στα πολυώνυμα. Μια άλλη προσέγγιση είναι η εξής:
Ας είναιπολυωνυμική εξίσωση με ρίζες τους
Τότε
(1)
Προκύπτει
οπότε γράφοντας τις αντίστοιχες για ταβρίσκουμε (με μικρή επιφύλαξη για τις πράξεις)
Εδώ αν γίνουν οι πράξεις, βλέπουμε ότι το πολυώνυμο που προκύπτει έχει παράγοντα τοκαι τελειώσαμε.
 (δεν ξέρω βέβαια αν αυτό το καθιστά NT)
(δεν ξέρω βέβαια αν αυτό το καθιστά NT)
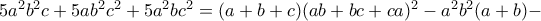





 και το ζητούμενο έπεται.
και το ζητούμενο έπεται.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης