 και τους πρώτους
και τους πρώτους  ώστε
ώστε  .
.Συντονιστές: cretanman, silouan, rek2
 και τους πρώτους
και τους πρώτους  ώστε
ώστε  .
.Καλησπέρα κύριε Θανάση!socrates έγραψε:Βρείτε το θετικό ακέραιοκαι τους πρώτους
ώστε
.
 .
.  . Τότε,
. Τότε, 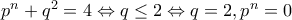 άτοπο.
άτοπο. . Τότε
. Τότε 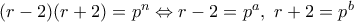 και
και  , οπότε
, οπότε 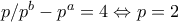 και εύκολα
και εύκολα 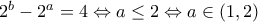 , με δεκτή
, με δεκτή 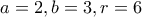 άτοπο (όχι πρώτος).
άτοπο (όχι πρώτος). . Τότε,
. Τότε, 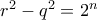 .
. , τότε
, τότε 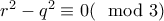 , συνεπώς
, συνεπώς 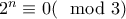 , άτοπο.
, άτοπο. ή
ή  .
.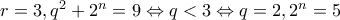 , άτοπο.
, άτοπο. και
και 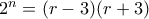 . Άρα,
. Άρα,  .
.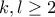 , τότε
, τότε 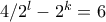 , άτοπο.
, άτοπο.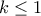 ή
ή 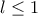 .
.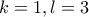 , και τελικά λύση την
, και τελικά λύση την 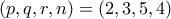 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες