 έχει
έχει  (θετικούς) διαιρέτες με συνολικό άθροισμα
(θετικούς) διαιρέτες με συνολικό άθροισμα  . Να βρεθούν όλες οι πιθανές τιμές του
. Να βρεθούν όλες οι πιθανές τιμές του  .
.Πηγή.
Συντονιστές: cretanman, silouan, rek2
 έχει
έχει  (θετικούς) διαιρέτες με συνολικό άθροισμα
(θετικούς) διαιρέτες με συνολικό άθροισμα  . Να βρεθούν όλες οι πιθανές τιμές του
. Να βρεθούν όλες οι πιθανές τιμές του  .
. και
και  . Αναζητούμε λοιπόν πρώτους αριθμούς
. Αναζητούμε λοιπόν πρώτους αριθμούς  ,
,  τέτοιους ώστε οι
τέτοιους ώστε οι  και
και  να διαιρούν τον
να διαιρούν τον  . Ήδη για
. Ήδη για  ο
ο  ισούται προς
ισούται προς  , άρα, από την
, άρα, από την  βλέπουμε ότι χρειάζεται να αναζητήσουμε είτε πρώτους
βλέπουμε ότι χρειάζεται να αναζητήσουμε είτε πρώτους  και πρώτους
και πρώτους  είτε να αναζητήσουμε λύσεις για
είτε να αναζητήσουμε λύσεις για  ή
ή  . Στην πρώτη περίπτωση εύκολα βλέπουμε -- μέσω διαιρετοτήτων -- ότι οι μόνες δυνατότητες είναι οι
. Στην πρώτη περίπτωση εύκολα βλέπουμε -- μέσω διαιρετοτήτων -- ότι οι μόνες δυνατότητες είναι οι  ,
,  ,
,  , που δίνουν αντίστοιχα
, που δίνουν αντίστοιχα 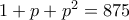 ,
,  ,
,  , όλες αδύνατες. Στην δεύτερη περίπτωση η
, όλες αδύνατες. Στην δεύτερη περίπτωση η  δίνει
δίνει  και
και  (πρώτος, εντάξει) ενώ η
(πρώτος, εντάξει) ενώ η  δίνει
δίνει  (δεν διαιρεί τον
(δεν διαιρεί τον  , απορρίπτεται).
, απορρίπτεται). ,
,  ,
,  . (Δημήτρη ... μήπως είναι 20 ετών το πρόβλημα;!)
. (Δημήτρη ... μήπως είναι 20 ετών το πρόβλημα;!) η οποία απορρίπτεται εύκολα.
η οποία απορρίπτεται εύκολα. μπορούμε να παρατηρήσουμε ότι το
μπορούμε να παρατηρήσουμε ότι το  είναι περιττός. Επίσης
είναι περιττός. Επίσης  το οποίο δεν είναι ποτέ πολλαπλάσιο του
το οποίο δεν είναι ποτέ πολλαπλάσιο του  . (Αφού τα μόνα τέλεια τετράγωνα
. (Αφού τα μόνα τέλεια τετράγωνα  είναι τα
είναι τα  .) Αναγκαστικά λοιπόν πρέπει
.) Αναγκαστικά λοιπόν πρέπει  και τα υπόλοιπα όπως τα έκανε ο Γιώργος.
και τα υπόλοιπα όπως τα έκανε ο Γιώργος.Πολύ πιθανόν. Εγώ όμως την πήρα από εδώ.gbaloglou έγραψε: (Δημήτρη ... μήπως είναι 20 ετών το πρόβλημα;!)
Καθορίζεται άραγε μονοσήμαντα ένας ακέραιος από το πλήθος των διαιρετών του και από το άθροισμα τους; Θα μπορούσαμε για παράδειγμα -- και με αφορμή το συγκεκριμένο πρόβλημα και την παραπάνω παρατήρηση -- να έχουμε πρώτουςDemetres έγραψε:Γιώργο, πρέπει να ελέγξεις και την περίπτωσηη οποία απορρίπτεται εύκολα.
 τέτοιους ώστε
τέτοιους ώστε  ; Εκ πρώτης όψεως ... δεν μου φαίνεται και τόσο απίθανο!
; Εκ πρώτης όψεως ... δεν μου φαίνεται και τόσο απίθανο!Όχι. Π.χ. οιgbaloglou έγραψε:
Καθορίζεται άραγε μονοσήμαντα ένας ακέραιος από το πλήθος των διαιρετών του και από το άθροισμα τους;
 και
και  έχουν από τέσσερις διαιρέτες και άθροισμα διαιρετών
έχουν από τέσσερις διαιρέτες και άθροισμα διαιρετών  .
. και
και  .
. διαιρέτες δεν το έψαξα όμως. [Βέβαια παράδειγμα με ακριβώς
διαιρέτες δεν το έψαξα όμως. [Βέβαια παράδειγμα με ακριβώς  διαιρέτες δεν υπάρχει διότι τότε ο
διαιρέτες δεν υπάρχει διότι τότε ο  είναι σίγουρα της μορφής
είναι σίγουρα της μορφής  και τότε το άθροισμα των διαιρετών καθορίζει και τον αριθμό.]
και τότε το άθροισμα των διαιρετών καθορίζει και τον αριθμό.] έχει ακριβώς έξι διαφορετικούς διαιρέτες, συμπεριλαμβανομένου του
έχει ακριβώς έξι διαφορετικούς διαιρέτες, συμπεριλαμβανομένου του  και του
και του  . Το γινόμενο των πέντε από αυτούς τους διαιρέτες ισούται με
. Το γινόμενο των πέντε από αυτούς τους διαιρέτες ισούται με  . Ποιος είναι ο έκτος διαιρέτης του
. Ποιος είναι ο έκτος διαιρέτης του  ;
;  ). Η ιδέα είναι να μην χρησιμοποιηθεί ο τύπος για το πλήθος των διαιρετών του
). Η ιδέα είναι να μην χρησιμοποιηθεί ο τύπος για το πλήθος των διαιρετών του  αλλά "με κοινό νου" να προσπερασθεί αυτό το σημείο. Δείτε όμως και το σχόλιο που βάζω στο τέλος της λύσης.
αλλά "με κοινό νου" να προσπερασθεί αυτό το σημείο. Δείτε όμως και το σχόλιο που βάζω στο τέλος της λύσης. έχει
έχει  διαιρέτες. Από αυτό συμπεραίνουμε ότι η ανάλυση του
διαιρέτες. Από αυτό συμπεραίνουμε ότι η ανάλυση του  σε πρώτους παράγοντες περιέχει το πολύ δύο διαφορετικούς πρώτους γιατί αν περιείχε τρεις ή περισσότερους, ας πούμε τους
σε πρώτους παράγοντες περιέχει το πολύ δύο διαφορετικούς πρώτους γιατί αν περιείχε τρεις ή περισσότερους, ας πούμε τους  και ενδεχομένως άλλους, τότε θα είχε τουλάχιστον
και ενδεχομένως άλλους, τότε θα είχε τουλάχιστον  διαιρέτες, τους
διαιρέτες, τους  και
και  . Άρα η ανάλυση του
. Άρα η ανάλυση του  σε πρώτους παράγοντες είναι είτε
σε πρώτους παράγοντες είναι είτε  (ένας πρώτος) ή
(ένας πρώτος) ή  (δύο πρώτοι). Από αυτό έπεται ότι, ακριβέστερα, ο
(δύο πρώτοι). Από αυτό έπεται ότι, ακριβέστερα, ο  είναι είτε της μορφής
είναι είτε της μορφής  με
με  διαιρέτες τους
διαιρέτες τους  (γενικότερα ο
(γενικότερα ο  έχει
έχει 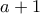 διαιρέτες) ή της μορφής
διαιρέτες) ή της μορφής  με
με  διαιρέτες, τους
διαιρέτες, τους 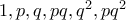 (εύκολα βλέπουμε ότι ο
(εύκολα βλέπουμε ότι ο  έχει μόνο τέσσερις διαιρέτες, τους
έχει μόνο τέσσερις διαιρέτες, τους  ενώ αν
ενώ αν  με
με  ή
ή  τότε έχουμε περισσότερους από 6 διαιρέτες: τους
τότε έχουμε περισσότερους από 6 διαιρέτες: τους  και άλλους ακόμη. Άρα μόνο η περίπτωση
και άλλους ακόμη. Άρα μόνο η περίπτωση  δίνει 6 διαιρέτες).
δίνει 6 διαιρέτες).  . Η ανάλυση του
. Η ανάλυση του  σε πρώτους παράγοντες είναι
σε πρώτους παράγοντες είναι  . Άρα δεν μπορεί
. Άρα δεν μπορεί  γιατί τότε το γινόμενο πέντε διαιρετών του (που υπενθυμίζουμε ότι οι διαιρέτες είναι οι
γιατί τότε το γινόμενο πέντε διαιρετών του (που υπενθυμίζουμε ότι οι διαιρέτες είναι οι  ) θα ήταν της μορφής
) θα ήταν της μορφής  . Όμως δεν μπορεί
. Όμως δεν μπορεί  (ίσον γινόμενο δύο διαφορετικών πρώτων) λόγω της μοναδικότητας της ανάλυσης αριθμών σε πρώτους παράγοντες. Τελικά
(ίσον γινόμενο δύο διαφορετικών πρώτων) λόγω της μοναδικότητας της ανάλυσης αριθμών σε πρώτους παράγοντες. Τελικά  . Ελέγχοντας όλες τις περιπτώσεις γινομένου πέντε διαιρετών του ώστε να συγκρίνουμε με τον
. Ελέγχοντας όλες τις περιπτώσεις γινομένου πέντε διαιρετών του ώστε να συγκρίνουμε με τον  θα διαπιστώσουμε ότι μόνο το
θα διαπιστώσουμε ότι μόνο το  (λείπει το
(λείπει το  ) είναι αυτής της μορφής με
) είναι αυτής της μορφής με  . Συνεπώς ο έκτος διαιρέτης είναι ο
. Συνεπώς ο έκτος διαιρέτης είναι ο  και ο
και ο  . Επαλήθευση: Το γινόμενο των πέντε από τους έξι διαιρέτες του
. Επαλήθευση: Το γινόμενο των πέντε από τους έξι διαιρέτες του  , συγκεκριμένα των
, συγκεκριμένα των  (όλοι πλην του
(όλοι πλην του  ) είναι
) είναι  .
.  σε πρώτους παράγοντες είναι
σε πρώτους παράγοντες είναι  , τότε το πλήθος των διαιρετών του
, τότε το πλήθος των διαιρετών του  είναι
είναι 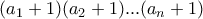 . Στα παραπάνω όπου είχαμε
. Στα παραπάνω όπου είχαμε  ή
ή  , το πλήθος των διαιρετών είναι
, το πλήθος των διαιρετών είναι 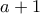 ή
ή  , αντίστοιχα. Με δεδομένο ότι ο
, αντίστοιχα. Με δεδομένο ότι ο  ως γινόμενο φυσικών γράφεται μόνο ως
ως γινόμενο φυσικών γράφεται μόνο ως  (ή με αντιμετάθεση αυτών) προκύπτουν μόνο οι περιπτώσεις
(ή με αντιμετάθεση αυτών) προκύπτουν μόνο οι περιπτώσεις  και
και  , όπως πριν.
, όπως πριν.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες