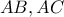 ενός ορθογωνίου και ισοσκελούς τριγώνου , ορίζουμε σημεία
ενός ορθογωνίου και ισοσκελούς τριγώνου , ορίζουμε σημεία 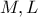 ,
,ώστε
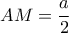 και
και 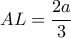 . Ο κύκλος
. Ο κύκλος 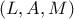 , τέμνει την υποτείνουσα
, τέμνει την υποτείνουσα  στα σημεία
στα σημεία  .
.Οι
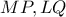 προεκτεινόμενες τέμνονται στο σημείο
προεκτεινόμενες τέμνονται στο σημείο  . Δείξτε ότι το
. Δείξτε ότι το  είναι τετράγωνο .
είναι τετράγωνο .Ο θεματοδότης θα είναι ευχαριστημένος , όταν οι ( διαφορετικές ) λύσεις ξεπεράσουν τις



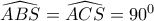 ..ενδιάμεσος στόχος ν.δ.ο
..ενδιάμεσος στόχος ν.δ.ο 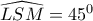 .. Με χρήση του σχήματος :
.. Με χρήση του σχήματος :
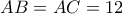 τότε
τότε 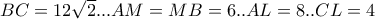 .Έστω
.Έστω 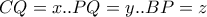
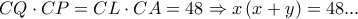
 ενώ
ενώ 
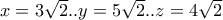 .Ακόμη είναι
.Ακόμη είναι  άρα ακτίνα
άρα ακτίνα 
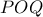 :
: 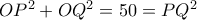 .
.  δηλ το
δηλ το 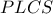 εγγράψιμο άρα
εγγράψιμο άρα 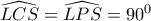 .
. 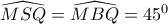 δηλ και το
δηλ και το  εγγράψιμο άρα
εγγράψιμο άρα 
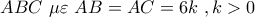 , το μέσο
, το μέσο  του
του  και το σημείο
και το σημείο  του
του  με
με 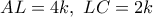 . Θεωρώ επίσης το συμμετρικό
. Θεωρώ επίσης το συμμετρικό  του
του  ως προς το
ως προς το  .
. που τέμνει την
που τέμνει την  στο
στο  και την ευθεία
και την ευθεία 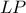 που τέμνει
που τέμνει  . Στο τρίγωνο
. Στο τρίγωνο  με διατέμνουσα την
με διατέμνουσα την  και το Θ.
και το Θ.  Αν τώρα από το
Αν τώρα από το  προφανώς
προφανώς 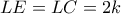
 Από τις
Από τις  έχουμε αβίαστα :
έχουμε αβίαστα : 
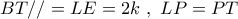
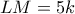 οπότε
οπότε 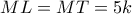 και άρα η
και άρα η 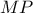 είναι μεσοκάθετος
είναι μεσοκάθετος  και διχοτόμος της
και διχοτόμος της  .
.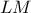 θα διέρχεται από το
θα διέρχεται από το  . Έστω τώρα ότι οι
. Έστω τώρα ότι οι 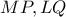 τέμνοντα στο
τέμνοντα στο 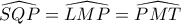 . Άρα το τετράπλευρο
. Άρα το τετράπλευρο 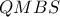 είναι εγγράψιμο
είναι εγγράψιμο 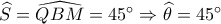 ( γιατί
( γιατί  ) , έτσι
) , έτσι  και ομοίως
και ομοίως 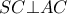 .
.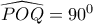 όπου
όπου  το μέσον του
το μέσον του  , κέντρο του εν λόγω κύκλου.
, κέντρο του εν λόγω κύκλου.
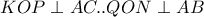 όπου τα
όπου τα  είναι οι τομές των ευθειών . Αρκεί δείξουμε ότι αυτά είναι σημεία και του κύκλου .
είναι οι τομές των ευθειών . Αρκεί δείξουμε ότι αυτά είναι σημεία και του κύκλου .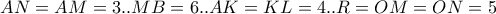
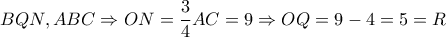
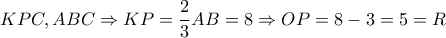
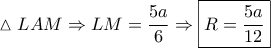
 οι ορθές προβολές των
οι ορθές προβολές των  αντίστοιχα επί της
αντίστοιχα επί της  με
με  μέσον της
μέσον της 
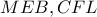 παίρνουμε
παίρνουμε 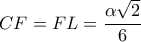 και
και 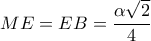
 του τραπεζίου
του τραπεζίου 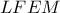 έχουμε
έχουμε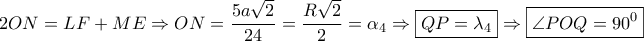
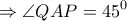
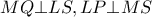 οπότε λόγω των εγγράψιμων
οπότε λόγω των εγγράψιμων 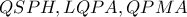 οι γωνίες
οι γωνίες  είναι ίσες όπως και οι γωνίες
είναι ίσες όπως και οι γωνίες  ,
,  εγγράψιμα
εγγράψιμα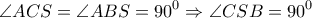 κι επειδή
κι επειδή 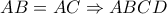 τετράγωνο
τετράγωνο