Ακέραιο Τρίγωνο!

Ορέστης Λιγνός · #1

Θεωρούμε τρίγωνο $\vartriangle ABC$ , του οποίου οι πλευρές έχουν μήκη πρώτους θετικούς ακεραίους αριθμούς.
Να δείξετε ότι το τρίγωνο δεν μπορεί να έχει ακέραιο εμβαδόν.

Διονύσιος Αδαμόπουλος · #2

Έστω

τα μήκη των τριών πλευρών.

Έστω

το εμβαδόν. Θα είναι από τον τύπο Ήρωνα:

(p+q+r)(p+q-r)(p+r-q)(r+q-p)=16E^2

(1)

Αν είναι $p, q, r\geq 3$ , θα είναι p, q, r

περιττοί, άρα και οι

όροι θα είναι περιττοί, άτοπο καθώς το δεξί μέλος είναι άρτιο. Έπεται λοιπόν πως ένας από τους πρώτους είναι ίσος με

, έστω

.

Παρατηρούμε πως δεν γίνεται να είναι όλοι οι άλλοι ίσοι με

, καθώς $6\cdot 2\cdot 2\cdot 2\cdot 2=16E^2\Leftrightarrow E^2=3$ , άτοπο.

Ούτε γίνεται να είναι δύο από αυτούς ίσοι με

, καθώς πάλι οι

όροι θα είναι περιττοί. Συνεπώς για τους άλλους πρώτους θα είναι $p, q\geq 3$ . Η σχέση (1) γίνεται:

(p+q+2)(p+q-2)(p+2-q)(q+2-p)=16E^2

Έστω πως $p, q\geq 5$ .

Διακρίνουμε τις εξής περιπτώσεις:

1) p=3n+1

και

Θα είναι

, άτοπο, καθώς το

διαιρεί το αριστερό μέλος σε περιττό βαθμό, ενώ το δεξί πρέπει να διαιρείται σε άρτιο.

2) p=3n+2

και

Θα είναι

, άτοπο, καθώς το

διαιρεί το αριστερό μέλος σε περιττό βαθμό, ενώ το δεξί πρέπει να διαιρείται σε άρτιο.

3) p=3n+1

και

(όμοια αντιμετωπίζεται η περίπτωση p=3n+2

και

)

Θα είναι (3n+3m+5)(3n+3m+1)(3n-3m+1)(3m+3-3n)=16E^2

, άτοπο, καθώς το

διαιρεί το αριστερό μέλος σε περιττό βαθμό, ενώ το δεξί πρέπει να διαιρείται σε άρτιο.

Άρα ένας από τους p, q

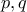να είναι

, έστω

.

Έστω $p\geq 5$

Θα είναι λοιπόν:

(p+5)(p+1)(p-1)(5-p)=16E^2

, άτοπο, καθώς το αριστερό μέλος είναι αρνητικό, ενώ το δεξί όχι.

Επομένως πρέπει p=3

, δηλαδή $8\cdot 4\cdot 2\cdot 2=16E^2\Leftrightarrow E^2=8$ , άτοπο.

Επομένως αφού εξαντλήσαμε όλα τα ενδεχόμενα συμπεράναμε πως πράγματι δεν υπάρχουν πρώτοι που να ικανοποιούν το ζητούμενο.

#3

Διονύσιος Αδαμόπουλος έγραψε: ↑
Κυρ Ιαν 14, 2018 8:53 pm
Έστω τα μήκη των τριών πλευρών.

Έστω το εμβαδόν. Θα είναι από τον τύπο Ήρωνα:

(1)

Αν είναι $p, q, r\geq 3$ , θα είναι περιττοί, άρα και οι όροι θα είναι περιττοί, άτοπο καθώς το δεξί μέλος είναι άρτιο. Έπεται λοιπόν πως ένας από τους πρώτους είναι ίσος με , έστω .

Παρατηρούμε πως δεν γίνεται να είναι όλοι οι άλλοι ίσοι με , καθώς $6\cdot 2\cdot 2\cdot 2\cdot 2=16E^2\Leftrightarrow E^2=3$ , άτοπο.

Ούτε γίνεται να είναι δύο από αυτούς ίσοι με , καθώς πάλι οι όροι θα είναι περιττοί. Συνεπώς για τους άλλους πρώτους θα είναι $p, q\geq 3$ . Η σχέση (1) γίνεται:

Από εδώ μπορούμε να το συνεχίσουμε και ως εξής:

Χωρίς βλάβη της γενικότητας είναι $p \geqslant q$ . Πρέπει q+2-p > 0

. Αλλά $q+2-p \leqslant 2$ . Οπότε p-q = 0

ή

. Επειδή οι p,q

είναι περιττοί, πρέπει p=q

. Τότε καταλήγουμε στην p^2 - 1 = E^2

η οποία είναι αδύνατη.

Ακέραιο Τρίγωνο!

Ακέραιο Τρίγωνο!

Re: Ακέραιο Τρίγωνο!

Re: Ακέραιο Τρίγωνο!

Μέλη σε σύνδεση