 ώστε
ώστε  .
.Συντονιστές: achilleas, emouroukos, silouan
 να είναι ακέραιος, δηλαδή ο
να είναι ακέραιος, δηλαδή ο  να είναι ακέραιος.
να είναι ακέραιος. και
και  είναι πρώτοι μεταξύ τους. Επομένως θέλουμε να βρούμε όλα τα
είναι πρώτοι μεταξύ τους. Επομένως θέλουμε να βρούμε όλα τα  , έτσι ώστε ο
, έτσι ώστε ο  να είναι ακέραιος. Προφανώς θα είναι θετικός ακέραιος, καθώς και ο αριθμητής και ο παρανομαστής είναι θετικοί ακέραιοι.
να είναι ακέραιος. Προφανώς θα είναι θετικός ακέραιος, καθώς και ο αριθμητής και ο παρανομαστής είναι θετικοί ακέραιοι. , με
, με  θετικός ακέραιος. Ελέγχουμε αρχικά την τετριμμένη περίπτωση
θετικός ακέραιος. Ελέγχουμε αρχικά την τετριμμένη περίπτωση  .
. . Όμως ξέρουμε πως
. Όμως ξέρουμε πως  , άρα
, άρα  .
. . Άρα
. Άρα  . Οι περιπτώσεις
. Οι περιπτώσεις  εγκρίνονται καθώς δίνουν τα
εγκρίνονται καθώς δίνουν τα  και
και  .
. .
. .
. , τότε θέλουμε ο
, τότε θέλουμε ο  να είναι ακέραιος, που όπως αναλύσαμε πρέπει
να είναι ακέραιος, που όπως αναλύσαμε πρέπει 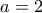 ή
ή  . Έχουμε λοιπόν τα
. Έχουμε λοιπόν τα  και
και 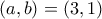
 , τότε θέλουμε ο
, τότε θέλουμε ο  να είναι ακέραιος, δηλαδή ο
να είναι ακέραιος, δηλαδή ο  να είναι ακέραιος, δηλαδή ο
να είναι ακέραιος, δηλαδή ο  να είναι ακέραιος, αφού όμως
να είναι ακέραιος, αφού όμως  , πρέπει
, πρέπει  να είναι ακέραιος, δηλαδή ο
να είναι ακέραιος, δηλαδή ο  να είναι ακέραιος, δηλαδή ο
να είναι ακέραιος, δηλαδή ο  να είναι ακέραιος, δηλαδή ο
να είναι ακέραιος, δηλαδή ο  να είναι ακέραιος, δηλαδή
να είναι ακέραιος, δηλαδή  ή
ή 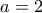 ή
ή  . Άρα έχουμε τα
. Άρα έχουμε τα 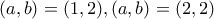 και
και  .
. , έχουμε πως πρέπει ο
, έχουμε πως πρέπει ο 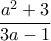 να είναι ακέραιος και με την ίδια διαδικασία προκύπτει το ισοδύναμο
να είναι ακέραιος και με την ίδια διαδικασία προκύπτει το ισοδύναμο 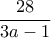 να είναι ακέραιος, άρα
να είναι ακέραιος, άρα  ή
ή  . Άρα έχουμε τα
. Άρα έχουμε τα  και
και  .
.
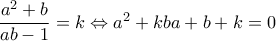 . Λύνοντας ως προς
. Λύνοντας ως προς  προκύπτει ότι η διακρίνουσα είναι ίση με
προκύπτει ότι η διακρίνουσα είναι ίση με  .
. ακέραιο πρέπει
ακέραιο πρέπει  . Είναι προφανές πως
. Είναι προφανές πως 
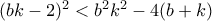 .
. , που ισχύει καθώς
, που ισχύει καθώς  και
και  .
.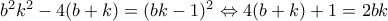 , άτοπο.
, άτοπο. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες