 για τους οποίους υπάρχουν μη μηδενικοί πραγματικοί αριθμοί
για τους οποίους υπάρχουν μη μηδενικοί πραγματικοί αριθμοί  ώστε
ώστε 
Συντονιστές: achilleas, emouroukos, silouan
 για τους οποίους υπάρχουν μη μηδενικοί πραγματικοί αριθμοί
για τους οποίους υπάρχουν μη μηδενικοί πραγματικοί αριθμοί  ώστε
ώστε 
 προφανώς δεν γίνεται. Για
προφανώς δεν γίνεται. Για  επίσης δεν γίνεται αφού τότε τα
επίσης δεν γίνεται αφού τότε τα  θα είναι ρίζες του πολυωνύμου
θα είναι ρίζες του πολυωνύμου  το οποίο όμως έχει μόνο μία πραγματική ρίζα. (Εδώ χρησιμοποιήσαμε τους τύπους του Vieta και το γεγονός ότι
το οποίο όμως έχει μόνο μία πραγματική ρίζα. (Εδώ χρησιμοποιήσαμε τους τύπους του Vieta και το γεγονός ότι 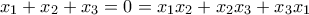 .)
.) . Παρατηρούμε ότι αν γίνεται για
. Παρατηρούμε ότι αν γίνεται για  , τότε γίνεται και για
, τότε γίνεται και για  θέτοντας επιπλέον
θέτοντας επιπλέον  .
. και
και  .
.  θέτουμε
θέτουμε  .
. θέτουμε
θέτουμε  ,
, 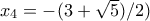 και
και  . Προφανώς
. Προφανώς 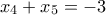 άρα
άρα 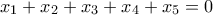 . Επίσης
. Επίσης  άρα
άρα  και άρα
και άρα  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες