 μη αρνητικοί να αποδείξετε οτι:
μη αρνητικοί να αποδείξετε οτι:
Συντονιστές: achilleas, emouroukos, silouan
 και έχουμε ισοδύναμα να αποδείξουμε ότι:
και έχουμε ισοδύναμα να αποδείξουμε ότι:
 Η αριστερή ανισότητα ισοδύναμα γίνεται:
Η αριστερή ανισότητα ισοδύναμα γίνεται:

 θα χρησιμοποιήσουμε την πολύ χρήσιμη ταυτότητα του Newton:
θα χρησιμοποιήσουμε την πολύ χρήσιμη ταυτότητα του Newton: 
 με τη βοήθεια των
με τη βοήθεια των  και στη συνέχεια την
και στη συνέχεια την  που χρειαζόμαστε.
που χρειαζόμαστε. γράφεται ισοδύναμα
γράφεται ισοδύναμα  δηλαδή ισοδύναμα
δηλαδή ισοδύναμα  δηλαδή ισοδύναμα
δηλαδή ισοδύναμα  που ισχύει από την γνωστή
που ισχύει από την γνωστή 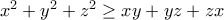
 Για τη δεξιά ανισότητα δε βρήκα κάτι κομψότερο από το παρακάτω:
Για τη δεξιά ανισότητα δε βρήκα κάτι κομψότερο από το παρακάτω: Αν
Αν  Μετά τις πράξεις και γράφοντας τη δεξιά ανισότητα με τη βοήθεια των
Μετά τις πράξεις και γράφοντας τη δεξιά ανισότητα με τη βοήθεια των 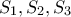 πρέπει να δείξουμε ότι:
πρέπει να δείξουμε ότι:
 :
: 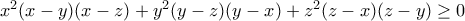 και γράφοντάς τη με τη βοήθεια των
και γράφοντάς τη με τη βοήθεια των 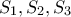 παίρνουμε:
παίρνουμε: απ' όπου
απ' όπου 
 αρκεί να δείξουμε ότι
αρκεί να δείξουμε ότι 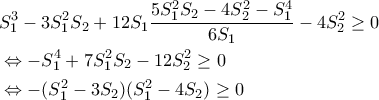
 , η τελευταία είναι αληθής όταν
, η τελευταία είναι αληθής όταν 
 Αν
Αν  δηλαδή
δηλαδή  η ανισότητα
η ανισότητα 

![\begin{aligned}LHS &= \left(x^2+y^2+z^2\right)(xy+yz+zx)+2(x^4+y^4+z^4) - 2(x^2y^2+y^2z^2+z^2x^2) - \left(x^2+y^2+z^2\right)^2 \\ &= \left(x^2+y^2+z^2\right)(xy+yz+zx) +(x^2+y^2+z^2)^2-6(x^2y^2+y^2z^2+z^2x^2) \\ &\stackrel{(3)}{>} 2(xy+yz+zx)^2+4(xy+yz+zx)^2-6(x^2y^2+y^2z^2+z^2x^2) \\ &=6\left[(xy+yz+zx)^2-x^2y^2-y^2z^2-z^2x^2\right] =6xyz(x+y+z)\geq 0\end{aligned} \begin{aligned}LHS &= \left(x^2+y^2+z^2\right)(xy+yz+zx)+2(x^4+y^4+z^4) - 2(x^2y^2+y^2z^2+z^2x^2) - \left(x^2+y^2+z^2\right)^2 \\ &= \left(x^2+y^2+z^2\right)(xy+yz+zx) +(x^2+y^2+z^2)^2-6(x^2y^2+y^2z^2+z^2x^2) \\ &\stackrel{(3)}{>} 2(xy+yz+zx)^2+4(xy+yz+zx)^2-6(x^2y^2+y^2z^2+z^2x^2) \\ &=6\left[(xy+yz+zx)^2-x^2y^2-y^2z^2-z^2x^2\right] =6xyz(x+y+z)\geq 0\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/e1f36914d941ecd8a52b24dbb60813d0.png)
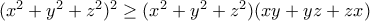 ;
;

Βασικά αφοτου κάνουμε πράξεις και φτάσουμε στην:ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Επειδη ειναι νωρίς θα γράψω σύντομα την λυση για την δεξιά.
Μετα απο μερικές πράξεις έχουμε να αποδείξουμε την:
Αν κάνουμε και άλλες πράξεις και Schur (2nd degree) στο LHS τότε η αποδεικτεα γράφεται:
Που ειναι εύκολο να αποδειχτεί με ΑΜ-ΓΜ.
JimNt. έγραψε:Βασικά αφοτου κάνουμε πράξεις και φτάσουμε στην:ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Επειδη ειναι νωρίς θα γράψω σύντομα την λυση για την δεξιά.
Μετα απο μερικές πράξεις έχουμε να αποδείξουμε την:
Αν κάνουμε και άλλες πράξεις και Schur (2nd degree) στο LHS τότε η αποδεικτεα γράφεται:
Που ειναι εύκολο να αποδειχτεί με ΑΜ-ΓΜ.
Απο
προκύπτει
. Συνεπώς, έχουμε να αποδείξουμε
, που είναι προφανης από Murihead...

Ναι οκ δεν είπα κάτι...ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:JimNt. έγραψε:Βασικά αφοτου κάνουμε πράξεις και φτάσουμε στην:ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Επειδη ειναι νωρίς θα γράψω σύντομα την λυση για την δεξιά.
Μετα απο μερικές πράξεις έχουμε να αποδείξουμε την:
Αν κάνουμε και άλλες πράξεις και Schur (2nd degree) στο LHS τότε η αποδεικτεα γράφεται:
Που ειναι εύκολο να αποδειχτεί με ΑΜ-ΓΜ.
Απο
προκύπτει
. Συνεπώς, έχουμε να αποδείξουμε
, που είναι προφανης από Murihead...
Και χωρις χρήση Murihead όπως το λέω γινεται:
Απο Schur
Χάρη σωστά! Στο σημείο που έφτασα:ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Θα σας γράψω για την πρωτη γιατι ειναι λίγο νωρίς...
Ελπίζω να ειμαι σωστός . . .
Η αριστερή δεν μπορεί να γίνει η προφανής
;
θα μπορούσα να έχω ολοκληρώσει τη λύση όπως λες. Στην πραγματικότητα όλη η μέθοδος που έκανα ήταν για να φτάσω ακριβώς στο ίδιο σημείο της παραγοντοποίησης λίγο πιο κάτω:cretanman έγραψε:Η αριστερή ανισότητα ισοδύναμα γίνεται:
Ας μείνει λόγω της μεθόδου που μας χρειάζεται για τη λύση της δεξιάς ανισότητας.cretanman έγραψε: ... δηλαδή ισοδύναμαπου ισχύει από την γνωστή
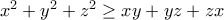

Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 7 επισκέπτες