Η τέταρτη ορθή

KARKAR · #1

: Η τέταρτη ορθή.png (11.72 KiB) Προβλήθηκε 741 φορές

Στο ορθογώνιο τρίγωνο $\displaystyle ABC , ( \hat{A}=90^0 )$ , η κάθετη στο άκρο

της υποτείνουσας

,

τέμνει την προέκταση της διχοτόμου

στο σημείο

, ενώ η κάθετη της πλευράς

στο ίχνος

της διχοτόμου , τέμνει τη

στο σημείο

. Δείξτε ότι $AP \perp AS$

Grigoris K. · #2

Καλησπέρα κ. Θανάση!

Φέρουμε $ST \perp CA$ , όπου το

ανήκει στην προέκταση του

. Παρατηρούμε ότι $\displaystyle{ \frac{BS}{CP} = \frac{ST}{CP} }$ .

Επίσης $\displaystyle{ \frac{ST}{AD} = \frac{CT}{AC} = \frac{BC}{AC}$ και $\displaystyle{ \frac{CP}{AD}} = \frac{BC}{AB}$ , άρα διαιρώντας κατά μέλη προκύπτει $\displaystyle{ \frac{ST}{CP} = \frac{AB}{AC} }$ .

Επομένως $\displaystyle{ \frac{BS}{CP} = \frac{AB}{AC} }$ . 'Ομως $\angle ABS = 90^o - \angle ABC = \angle ACP$ . Άρα $\displaystyle{ \triangle ABS \sim \triangle ACP }$ .

Συνεπώς $\displaystyle{ APBS }$ εγγράψιμο και ισχύει $\displaystyle{ \angle PAS = 90^o }$ .

#3

KARKAR έγραψε:Στο ορθογώνιο τρίγωνο $\displaystyle ABC , ( \hat{A}=90^0 )$ , η κάθετη στο άκρο της υποτείνουσας ,τέμνει την προέκταση της διχοτόμου στο σημείο , ενώ η κάθετη της πλευράς στο ίχνος της διχοτόμου , τέμνει τη στο σημείο . Δείξτε ότι $AP \perp AS$

: Η τέταρτη κορυφή..png (27.46 KiB) Προβλήθηκε 713 φορές

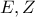Έστω οι ορθές προβολές των στην και η προβολή του στην . Με διχοτόμο της $\angle C$ είναι $\boxed{DA = DZ}:\left( 1 \right)$ και

$\angle SDB\mathop = \limits^{\kappa .\kappa o\rho \upsilon \varphi \eta \nu } \angle SDA = \angle SDZ\mathop = \limits^{DZ\parallel SB} \angle DSB \Rightarrow \boxed{BS = BD}:\left( 2 \right)$ . Είναι $\dfrac{{AD}}{{FB}}\mathop = \limits^{\left( 1 \right)} \dfrac{{DZ}}{{AE}}\mathop = \limits^{DZ\parallel AE} \dfrac{{BD}}{{BA}}\mathop = \limits^{\left( 2 \right)} \dfrac{{BS}}{{BA}} \Rightarrow \boxed{\dfrac{{AD}}{{FB}} = \dfrac{{BS}}{{BA}}}:\left( 3 \right)$ .

Από τη σχέση $\left( 3 \right)$ σύμφωνα με το Stathis Koutras' Theorem προκύπτει ότι $PA \bot AS$ και το ζητούμενο έχει αποδειχθεί..

Στάθης

Υ.Σ. Η παραπάνω λύση αφιερώνεται με εκτίμηση στον καταπληκτικό Γρηγόρη Κακλαμάνο , που με μεγάλη μου χαρά βλέπω πως επανήλθε στο
(μας έλλειψες αρκετά Γρηγόρη μου) και άρχισε να "σκουπίζει" τις ασκήσεις

#4

Είναι εύκολο να δούμε ότι λόγω της παραλληλίας των $AC\,\,\kappa \alpha \iota \,\,DP$ και της

διχοτόμου

το τρίγωνο PCD

είναι ισοσκελές δηλαδή $PC = PD\,\,(1)$ . Αλλά και το

τρίγωνο BDS

είναι ισοσκελές ( $BD = BS\,\,\,(2)$ ) γιατί οι γωνίες του στα D,S

είναι

συμπληρώματα της γωνίας $\widehat {ACD} = \widehat {DCB} = \widehat \theta$ .

Επίσης $\boxed{\widehat {ACP} = \widehat {ABS} = 2\widehat \theta }\,\,\,(3)$ ως συμπληρώματα της $\widehat \omega$ .

: Τέταρτη ορθή.png (27.05 KiB) Προβλήθηκε 687 φορές

Μετά απ’ αυτά διαδοχικά και λόγω των $(1)\,,\,\,(2)$ και της ομοιότητας

$\vartriangle DBP \approx \vartriangle ABC$ έχουμε:

$\dfrac{{BS}}{{BA}} = \dfrac{{BD}}{{BA}} = \dfrac{{PD}}{{CA}} = \dfrac{{CP}}{{CA}}$ δηλαδή $\boxed{\dfrac{{BS}}{{BA}} = \dfrac{{CP}}{{CA}}}$ που λόγω της (3)

μας εξασφαλίζει την

Ομοιότητα : $\vartriangle BAS \approx \vartriangle CAP \Rightarrow \boxed{\widehat {BSA} = \widehat {CPA}}$ οπότε το τετράπλευρο ASBP

είναι

εγγράψιμο άρα $AS \bot AP$ .

Φιλικά, Νίκος

Βλέπω ο νεαρός Γρηγόρης ( Μας θυμήθηκες Μπράβο!) μ' έχει υπερφαλαγγίσει!

Η τέταρτη ορθή

Η τέταρτη ορθή

Re: Η τέταρτη ορθή

Re: Η τέταρτη ορθή

Re: Η τέταρτη ορθή

Μέλη σε σύνδεση