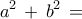 σταθερό τότε να βρείτε το μέγιστο της παράστασης
σταθερό τότε να βρείτε το μέγιστο της παράστασης
GIORGARAS έγραψε:Ανσταθερό τότε να βρείτε το μέγιστο της παράστασης
 .
. είναι σταθερό (αφού είναι και το
είναι σταθερό (αφού είναι και το  ), άρα είναι και το ζητούμενο μέγιστο.
), άρα είναι και το ζητούμενο μέγιστο. .
. και
και  ,
,  σταθερό.
σταθερό. είναι οι κάθετες πλευρές ορθογωνίου τριγώνου πλευράς
είναι οι κάθετες πλευρές ορθογωνίου τριγώνου πλευράς  .
.  διατρέχουν το
διατρέχουν το  , στην απάντησή μας ότι η ισότητα ισχύει όταν
, στην απάντησή μας ότι η ισότητα ισχύει όταν  , χρειάζεται και η προσθήκη
, χρειάζεται και η προσθήκη 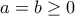 ;
; , μέγιστο του
, μέγιστο του  , έχουμε για
, έχουμε για 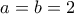 κι όχι για
κι όχι για  .
.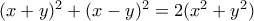
 είναι σταθερό , πότε το άθροισμα
είναι σταθερό , πότε το άθροισμα 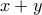 γίνεται μέγιστο ;
γίνεται μέγιστο ;Γιώργο την καλημέρα μου ..Γιώργος Ρίζος έγραψε: Επίσης, μια ερώτηση:
Εφόσον δεχόμαστε ότι ταδιατρέχουν το
, στην απάντησή μας ότι η ισότητα ισχύει όταν
, χρειάζεται και η προσθήκη
;
Π.χ. αν, μέγιστο του
, έχουμε για
κι όχι για
.

α)KARKAR έγραψε:Σε παλιότερη έκδοση (2004) του σχολικού βιβλίου της Άλγεβρας Α' , υπήρχε η εξής άσκηση :
α) Δείξτε ότι :
β) Αν το άθροισμαείναι σταθερό , πότε το άθροισμα
γίνεται μέγιστο ;
 (1)
(1) σταθερός μη αρνητικός αριθμός.
σταθερός μη αρνητικός αριθμός. . Τότε
. Τότε 
 παίρνει τη μέγιστη τιμή του "όταν οι
παίρνει τη μέγιστη τιμή του "όταν οι 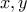 είναι ίσοι", αλλά όταν
είναι ίσοι", αλλά όταν  .
.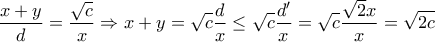
 , μα τότε κόκκινο ισοσκελές άρα
, μα τότε κόκκινο ισοσκελές άρα 

Κανονικά θα έπρεπε να εμπλουτιστούν τα βιβλία με τέτοιου είδους προβλήματα που μπορούν να έχουν όμορφες γεωμετρικές ερμηνείες, αλγεβρικές γενικεύσεις και γενικότερα που θα σηκώνουν περαιτέρω συζήτηση σε διάφορα επίπεδα και θα δουλεύουν προπαρασκευαστικά για αργότερα.KARKAR έγραψε:Σε παλιότερη έκδοση (2004) του σχολικού βιβλίου της Άλγεβρας Α' , υπήρχε η εξής άσκηση :
α) Δείξτε ότι :
β) Αν το άθροισμαείναι σταθερό , πότε το άθροισμα
γίνεται μέγιστο ;
Αυτή η έκδοση είχε και άλλες ωραίες εφαρμογές , που απεθύνονταν βέβαια σε μαθητές
που θέλουν "κάτι παραπάνω" , δυστυχώς στις νεότερες εκδόσεις αποσύρθηκαν ...
 με νόρμα ευκλείδειος είναι να ικανοποιείται για κάθε σημείο
με νόρμα ευκλείδειος είναι να ικανοποιείται για κάθε σημείο  του χώρου η σχέση
του χώρου η σχέση 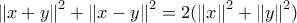
 , το
, το  κινείται
κινείται στην προέκταση της
στην προέκταση της  , ώστε :
, ώστε :  , λόγω της
, λόγω της  , το
, το  κινείται σε κύκλο , με κέντρο το μέσο του ημικυκλίου , οπότε
κινείται σε κύκλο , με κέντρο το μέσο του ημικυκλίου , οπότε 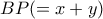 μεγιστοποιείται όταν η
μεγιστοποιείται όταν η 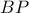 γίνει διάμετρος και τότε :
γίνει διάμετρος και τότε : 
 είναι ίσα (που συμβαίνει σε δύο περιπτώσεις που ικανοποιούν την υπόθεση), αλλά και ότι χρειάζεται να γράφουμε και την θετική τιμή που παίρνουν.
είναι ίσα (που συμβαίνει σε δύο περιπτώσεις που ικανοποιούν την υπόθεση), αλλά και ότι χρειάζεται να γράφουμε και την θετική τιμή που παίρνουν.Christos.N έγραψε:Γιώργο την καλημέρα μου ..Γιώργος Ρίζος έγραψε: Επίσης, μια ερώτηση:
Εφόσον δεχόμαστε ότι ταδιατρέχουν το
, στην απάντησή μας ότι η ισότητα ισχύει όταν
, χρειάζεται και η προσθήκη
;
Προφανώς όχι

 .
. είναι θετικά(ή μηδέν), και αφού είναι ίσα μεταξύ τους, η μόνη τιμή που επαληθεύει την υπόθεση είναι
είναι θετικά(ή μηδέν), και αφού είναι ίσα μεταξύ τους, η μόνη τιμή που επαληθεύει την υπόθεση είναι  .
. σταθερό τότε να βρείτε το μέγιστο της παράστασης
σταθερό τότε να βρείτε το μέγιστο της παράστασης  .
. . Τότε
. Τότε  .
. .
. .
. που να ικανοποιούν την αρχική σχέση, πρέπει
που να ικανοποιούν την αρχική σχέση, πρέπει  , οπότε είναι
, οπότε είναι 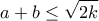 .
.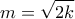 δηλαδή όταν
δηλαδή όταν  .
. όπου
όπου 
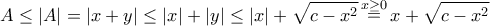
![\displaystyle{\begin{array}{l}
f\left( x \right) = x + \sqrt {c - {x^2}} ,0 \le x \le \sqrt c \\
x \in \left( {0,\sqrt c } \right):f'\left( x \right) = 1 - \frac{x}{{\sqrt {c - {x^2}} }} \Rightarrow \left\{ \begin{array}{l}
f'\left( x \right) < 0 \Leftrightarrow x > \sqrt {\frac{c}{2}} \\
\\
f'\left( x \right) > 0 \Leftrightarrow x < \sqrt {\frac{c}{2}}
\end{array} \right.\mathop \Rightarrow \limits^{f \in C\left[ {0,\sqrt {\frac{c}{2}} } \right]} f\left( x \right) \le f\left( {\sqrt {\frac{c}{2}} } \right) = \sqrt {2c}
\end{array}} \displaystyle{\begin{array}{l}
f\left( x \right) = x + \sqrt {c - {x^2}} ,0 \le x \le \sqrt c \\
x \in \left( {0,\sqrt c } \right):f'\left( x \right) = 1 - \frac{x}{{\sqrt {c - {x^2}} }} \Rightarrow \left\{ \begin{array}{l}
f'\left( x \right) < 0 \Leftrightarrow x > \sqrt {\frac{c}{2}} \\
\\
f'\left( x \right) > 0 \Leftrightarrow x < \sqrt {\frac{c}{2}}
\end{array} \right.\mathop \Rightarrow \limits^{f \in C\left[ {0,\sqrt {\frac{c}{2}} } \right]} f\left( x \right) \le f\left( {\sqrt {\frac{c}{2}} } \right) = \sqrt {2c}
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/25bad1c52ae99896359192fd6f6d6bfc.png)
 επιτυγχάνεται όταν
επιτυγχάνεται όταν 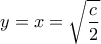 και είναι
και είναι  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες