 συνεχής σ' ένα διάστημα
συνεχής σ' ένα διάστημα  .
. Αν
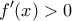 για κάθε εσωτερικό σημείο
για κάθε εσωτερικό σημείο  του
του  , να αποδείξετε ότι η
, να αποδείξετε ότι η  είναι γνησίως αύξουσα σε όλο το
είναι γνησίως αύξουσα σε όλο το  .
.β) Θεωρούμε παραγωγίσιμη συνάρτηση
 τέτοια, ώστε :
τέτοια, ώστε : για κάθε
για κάθε  με
με  .
.i) Να αποδείξετε ότι
 .
.ii) Να μελετήσετε ως προς τη μονοτονία τη συνάρτηση
 .
. 2. α) Δίνεται ο πίνακας
![\displaystyle{A= \left[ \begin{matrix}
\beta & -1 \\
\beta & -2 \\
\end{matrix} \right]} \displaystyle{A= \left[ \begin{matrix}
\beta & -1 \\
\beta & -2 \\
\end{matrix} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/cc79c6bed2726c03949038df55ae740b.png) , όπου
, όπου  .
.Αν
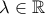 , θεωρούμε το
, θεωρούμε το  γραμμικό σύστημα
γραμμικό σύστημα  όπου
όπου ![\displaystyle{X= \left[ \begin{matrix}
x \\
y \\
\end{matrix} \right]} \displaystyle{X= \left[ \begin{matrix}
x \\
y \\
\end{matrix} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/947e0e025a4de022eb3fa073f0489ae8.png) είναι ο πίνακας-στήλη των αγνώστων.
είναι ο πίνακας-στήλη των αγνώστων.Να αποδείξετε ότι για κάθε
 υπάρχουν ακριβώς δύο τιμές του
υπάρχουν ακριβώς δύο τιμές του 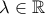 ,
,για τις οποίες το παραπάνω γραμμικό σύστημα έχει και μη μηδενικές λύσεις.
β) Έστω
 ένας
ένας  πίνακας για τον οποίο ισχύει
πίνακας για τον οποίο ισχύει ![\displaystyle{A= \left[ \begin{matrix}
2+\left| A \right| & 4\left| A \right|+1 \\
1 & 2\left| A \right| \\
\end{matrix} \right]} \displaystyle{A= \left[ \begin{matrix}
2+\left| A \right| & 4\left| A \right|+1 \\
1 & 2\left| A \right| \\
\end{matrix} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/c7923254b1b6a762859ba75dbff5afa9.png)
και
 όπου
όπου  είναι η ορίζουσα του πίνακα
είναι η ορίζουσα του πίνακα  .
.i) Να αποδείξετε ότι
![\displaystyle{A=\left[ \begin{matrix}
3 & 5 \\
1 & 2 \\
\end{matrix} \right]} \displaystyle{A=\left[ \begin{matrix}
3 & 5 \\
1 & 2 \\
\end{matrix} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/836d090b1ee23e84ba60f6542008d04d.png)
ii) Να αποδείξετε ότι ο πίνακας
 , όπου
, όπου  ο
ο  μοναδιαίος πίνακας, είναι αντίστροφος του
μοναδιαίος πίνακας, είναι αντίστροφος του 
και να βρείτε τον πίνακα
 για τον οποίο ισχύει
για τον οποίο ισχύει 
3. α) Θεωρούμε συνάρτηση
 συνεχή στο
συνεχή στο  .
.i) Να αποδείξετε ότι

ii) Έστω ότι

Να αποδείξετε ότι υπάρχει ένα τουλάχιστον
 τέτοιο, ώστε
τέτοιο, ώστε  .
.β) Θεωρούμε συνεχή συνάρτηση
 που ικανοποιεί την ισότητα
που ικανοποιεί την ισότητα .
.i) Nα αποδείξετε ότι

ii) Να βρείτε την εξίσωση της εφαπτόμενης της γραφικής παράστασης της
 στο σημείο της
στο σημείο της  .
.4. α) Θεωρούμε τη συνάρτηση
 με
με  .
.i) Να αποδείξετε ότι η εξίσωση
 με
με  παριστάνει κύκλο και να βρείτε το κέντρο και την ακτίνα του.
παριστάνει κύκλο και να βρείτε το κέντρο και την ακτίνα του.ii) Να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται από τη γραφική παράσταση της
 και τον άξονα
και τον άξονα  .
.β) Έστω
 είναι ο δειγματικός χώρος ενός πειράματος τύχης και
είναι ο δειγματικός χώρος ενός πειράματος τύχης και  ενδεχόμενα του τέτοια, ώστε
ενδεχόμενα του τέτοια, ώστε  .
.Έστω
 είναι οι πιθανότητες των
είναι οι πιθανότητες των  αντίστοιχα.
αντίστοιχα. Έστω ότι οι πραγματικοί αριθμοί
 είναι θέσεις τοπικών ακροτάτων της συνάρτησης
είναι θέσεις τοπικών ακροτάτων της συνάρτησης  , με
, με  .
.Να υπολογίσετε
i) τις πιθανότητες

ii) τις πιθανότητες
 και
και  όπου
όπου  το αντίθετο ενδεχόμενο του
το αντίθετο ενδεχόμενο του  .
.
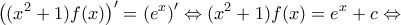
 . Όμως
. Όμως 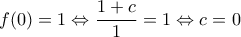 και
και 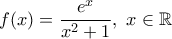 .
. .
.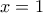 άρα η συνάρτηση είναι γνησίως αύξουσα στο
άρα η συνάρτηση είναι γνησίως αύξουσα στο 
 . Θέτουμε
. Θέτουμε  και έτσι
και έτσι  .
. .
.  η οποία είναι παραγωγίσιμη στο
η οποία είναι παραγωγίσιμη στο ![\displaystyle{[1,7]} \displaystyle{[1,7]}](/forum/ext/geomar/texintegr/latexrender/pictures/5c7565ded6fc1b344687bd56d2529a50.png) άρα
άρα τέτοιο ώστε
τέτοιο ώστε  .
.![\displaystyle{\int_0^1 (t^2+t)dt=\big[\frac{t^3}{3}+\frac{t^2}{2}\big]_0^1=\frac{1}{3}+\frac{1}{2}=\frac{5}{6}} \displaystyle{\int_0^1 (t^2+t)dt=\big[\frac{t^3}{3}+\frac{t^2}{2}\big]_0^1=\frac{1}{3}+\frac{1}{2}=\frac{5}{6}}](/forum/ext/geomar/texintegr/latexrender/pictures/66a3ca6d4d617c7f50d869bc679671f2.png) επομένως η δοσμένη σχέση γίνεται:
επομένως η δοσμένη σχέση γίνεται: . Τα μέλη της τελευταίας είναι παραγωγίσιμες συναρτήσεις
. Τα μέλη της τελευταίας είναι παραγωγίσιμες συναρτήσεις .
. άρα
άρα 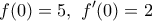 και η εξίσωση είναι :
και η εξίσωση είναι :
![\displaystyle{AX = \lambda X \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
\beta &{ - 1}\\
\beta &{ - 2}
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\lambda x}\\
{\lambda y}
\end{array}} \right] \Leftrightarrow \left\{ \begin{array}{l}
\beta x - y = \lambda x\\
\beta x - 2y = \lambda y
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
\left( {\beta - \lambda } \right)x - y = 0\\
\beta x - \left( {2 + \lambda } \right)y = 0
\end{array} \right.} \displaystyle{AX = \lambda X \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
\beta &{ - 1}\\
\beta &{ - 2}
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\lambda x}\\
{\lambda y}
\end{array}} \right] \Leftrightarrow \left\{ \begin{array}{l}
\beta x - y = \lambda x\\
\beta x - 2y = \lambda y
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
\left( {\beta - \lambda } \right)x - y = 0\\
\beta x - \left( {2 + \lambda } \right)y = 0
\end{array} \right.}](/forum/ext/geomar/texintegr/latexrender/pictures/cba60cf6aa5d6514c462146b73568e96.png)

 (1)
(1) διακρίνουσα
διακρίνουσα  για κάθε
για κάθε 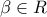


 αφού
αφού 
![{A^2} = \left[ {\begin{array}{*{20}{c}}
3&5\\
1&2
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
3&5\\
1&2
\end{array}} \right] \Rightarrow {A^2} = \left[ {\begin{array}{*{20}{c}}
{14}&{25}\\
5&9
\end{array}} \right] {A^2} = \left[ {\begin{array}{*{20}{c}}
3&5\\
1&2
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
3&5\\
1&2
\end{array}} \right] \Rightarrow {A^2} = \left[ {\begin{array}{*{20}{c}}
{14}&{25}\\
5&9
\end{array}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/c86151bb7ffa62545f76b0ccda6121cc.png)
![B = 5I - A\mathop \Rightarrow \limits^{ \cdot A} AB = 5A - {A^2} \Rightarrow AB = \left[ {\begin{array}{*{20}{c}}
{15}&{25}\\
5&{10}
\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}
{14}&{25}\\
5&9
\end{array}} \right] \Rightarrow B = 5I - A\mathop \Rightarrow \limits^{ \cdot A} AB = 5A - {A^2} \Rightarrow AB = \left[ {\begin{array}{*{20}{c}}
{15}&{25}\\
5&{10}
\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}
{14}&{25}\\
5&9
\end{array}} \right] \Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/c1952e124a18f9d3a4e92bcf1f05a078.png)
![AB = \left[ {\begin{array}{*{20}{c}}
1&0\\
0&1
\end{array}} \right] \Rightarrow AB = I \Rightarrow {A^{ - 1}} = B AB = \left[ {\begin{array}{*{20}{c}}
1&0\\
0&1
\end{array}} \right] \Rightarrow AB = I \Rightarrow {A^{ - 1}} = B](/forum/ext/geomar/texintegr/latexrender/pictures/024813a48aeb52fe5685a977e5c9e3b0.png)
![BX = A\mathop \Leftrightarrow \limits^{ \cdot A} ABX = {A^2}\mathop \Leftrightarrow \limits^{AB = I} X = \left[ {\begin{array}{*{20}{c}}
{14}&{25}\\
5&9
\end{array}} \right] BX = A\mathop \Leftrightarrow \limits^{ \cdot A} ABX = {A^2}\mathop \Leftrightarrow \limits^{AB = I} X = \left[ {\begin{array}{*{20}{c}}
{14}&{25}\\
5&9
\end{array}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/6c48bd05988dc1564d63cd67318fb915.png)



 που σημαίνει ότι για κάθε
που σημαίνει ότι για κάθε  υπάρχουν δύο τιμές του
υπάρχουν δύο τιμές του 
 ή
ή  κι αφού
κι αφού 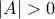 τότε
τότε  άρα
άρα ![B=\left[ \begin{matrix}
2 & -5 \\
-1 & 3 \\
\end{matrix} \right] B=\left[ \begin{matrix}
2 & -5 \\
-1 & 3 \\
\end{matrix} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/738d04bfefe33f4714d8f5c1d1064415.png) και
και ![BA=\left[ \begin{matrix}
3\cdot 2-5\cdot1 & 2\cdot5-5\cdot2 \\
-1\cdot3+3\cdot1 & -1\cdot5+3\cdot2 \\
\end{matrix} \right]=I BA=\left[ \begin{matrix}
3\cdot 2-5\cdot1 & 2\cdot5-5\cdot2 \\
-1\cdot3+3\cdot1 & -1\cdot5+3\cdot2 \\
\end{matrix} \right]=I](/forum/ext/geomar/texintegr/latexrender/pictures/f9c7c1d346d409f738ddbfa9cde2a77f.png) άρα
άρα 
![BX=A\Leftrightarrow A(BX)=A^2\Leftrightarrow (AB)X=A^2\Leftrightarrow X=A^2=\left[ \begin{matrix}
14 & 25 \\
8 & 9 \\
\end{matrix} \right]} BX=A\Leftrightarrow A(BX)=A^2\Leftrightarrow (AB)X=A^2\Leftrightarrow X=A^2=\left[ \begin{matrix}
14 & 25 \\
8 & 9 \\
\end{matrix} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/81f406380ddf5c5d4db4546fa76351aa.png)

 παριστάνει κύκλο με κέντρο
παριστάνει κύκλο με κέντρο  και ακτίνα
και ακτίνα  .
.

![\displaystyle E = \int_3^1 {f\left( x \right)dx} = \left[ {\frac{{{x^3}}}{3} - 2{x^2} + 3x} \right]_3^1 = \frac{1}{3} - 2 + 3 - 9 + 18 - 9 = \frac{4}{3}\tau .\mu . \displaystyle E = \int_3^1 {f\left( x \right)dx} = \left[ {\frac{{{x^3}}}{3} - 2{x^2} + 3x} \right]_3^1 = \frac{1}{3} - 2 + 3 - 9 + 18 - 9 = \frac{4}{3}\tau .\mu .](/forum/ext/geomar/texintegr/latexrender/pictures/b563c6fdbc1b9a99141ade9735d68e2a.png)
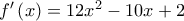

 είναι γν. αύξουσα στα διαστήματα
είναι γν. αύξουσα στα διαστήματα ![\displaystyle\left( { - \infty ,\frac{1}{3}} \right] \displaystyle\left( { - \infty ,\frac{1}{3}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/672b6521810633d62244c4193c49219c.png) και
και  και γν. φθίνουσα στο διάστημα
και γν. φθίνουσα στο διάστημα ![\displaystyle\left[ {\frac{1}{3},\frac{1}{2}} \right] \displaystyle\left[ {\frac{1}{3},\frac{1}{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/51da24d48babb11709dde4eba95d334e.png) .
.

 και
και 


