 είναι
είναι  πίνακες και
πίνακες και  είναι ένας
είναι ένας  αντιστρέψιμος πίνακας .
αντιστρέψιμος πίνακας . Να αποδείξετε ότι ισχύει η ισοδυναμία

β) Αν
 , να αποδείξετε ότι υπάρχουν πραγματικοί αριθμοί
, να αποδείξετε ότι υπάρχουν πραγματικοί αριθμοί  και
και  ,
, ώστε να ισχύει η σχέση :
![\displaystyle{\left[ \begin{matrix}
\lambda & 2 \\
-2 & \lambda \\
\end{matrix} \right]\cdot \left[ \begin{matrix}
x \\
y \\
\end{matrix} \right]+\left[ \begin{matrix}
-2 & \lambda \\
\lambda & -1 \\
\end{matrix} \right]\cdot \left[ \begin{matrix}
x \\
y \\
\end{matrix} \right]=\mathsf{\lambda }\left[ \begin{matrix}
1 \\
1 \\
\end{matrix} \right]+\left[ \begin{matrix}
1 \\
-3 \\
\end{matrix} \right]} \displaystyle{\left[ \begin{matrix}
\lambda & 2 \\
-2 & \lambda \\
\end{matrix} \right]\cdot \left[ \begin{matrix}
x \\
y \\
\end{matrix} \right]+\left[ \begin{matrix}
-2 & \lambda \\
\lambda & -1 \\
\end{matrix} \right]\cdot \left[ \begin{matrix}
x \\
y \\
\end{matrix} \right]=\mathsf{\lambda }\left[ \begin{matrix}
1 \\
1 \\
\end{matrix} \right]+\left[ \begin{matrix}
1 \\
-3 \\
\end{matrix} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e05bfc6913abfc7414e1bc33ebafff26.png) .
.2. α) Στην τελευταία Διεθνή Μαθηματική Ολυμπιάδα , που έγινε στη Βομβάη , πέντε Έλληνες μαθητές βραβεύτηκαν με μετάλλια.
Η Ελληνική Μαθηματική Εταιρεία αποφάσισε να δωρίσει σε καθένα από τους πέντε μαθητές από δυο βιβλία,
που επιλέγονται από μια συλλογή δέκα διαφορετικών βιβλίων.
Με πόσους διαφορετικούς τρόπους τα δέκα αυτά βιβλία μπορούν να διανεμηθούν στους πέντε βραβευθέντες μαθητές;
β) Θεωρούμε το σύνολο των θετικών ακεραίων αριθμών
 τέτοιων ώστε
τέτοιων ώστε 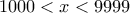 .
. Ως γνωστόν αυτοί είναι τετραψήφιοι αριθμοί στο δεκαδικό σύστημα αρίθμησης.
Πόσοι από αυτούς τους αριθμούς γράφονται με τέσσερα διαφορετικά ψηφία;
3. α) Αν οι συναρτήσεις
 είναι δυο φορές παραγωγίσιμες στο
είναι δυο φορές παραγωγίσιμες στο  και ικανοποιούν τις σχέσεις :
και ικανοποιούν τις σχέσεις :
 για κάθε
για κάθε 




i) Να βρείτε τη συνάρτηση

ii) Να βρείτε το εμβαδόν του χωρίου που περικλείεται από τις γραφικές παραστάσεις των συναρτήσεων
 και
και  .
.β) Έστω
 πραγματική συνάρτηση ορισμένη στο
πραγματική συνάρτηση ορισμένη στο  που είναι δυο φορές παραγωγίσιμη και ισχύει
που είναι δυο φορές παραγωγίσιμη και ισχύει 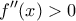 για κάθε
για κάθε  .
.Έστω
 και
και 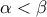 . Να αποδειχθεί ότι :
. Να αποδειχθεί ότι :i)
 για κάθε
για κάθε ![\displaystyle{x\in [ \alpha,\beta]} \displaystyle{x\in [ \alpha,\beta]}](/forum/ext/geomar/texintegr/latexrender/pictures/f65b01c9498e2185fb6dfee049d85148.png)
ii)
 .
.4. Έστω
 πραγματική συνάρτηση συνεχής στο
πραγματική συνάρτηση συνεχής στο  τέτοια ώστε
τέτοια ώστε  για κάθε
για κάθε  .
. Θεωρούμε τη συνάρτηση
 .
.α) Να αποδείξετε ότι

β) Να αποδείξετε ότι η εξίσωση
 έχει μια μόνο ρίζα στο διάστημα
έχει μια μόνο ρίζα στο διάστημα  .
.



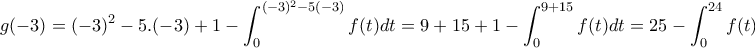


 είναι συνεχής στο
είναι συνεχής στο ![\displaystyle{[0,24]} \displaystyle{[0,24]}](/forum/ext/geomar/texintegr/latexrender/pictures/c0d943116f10bcd5192f5e8f903b4906.png)

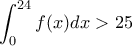 συνεπώς αποδείξαμε ότι
συνεπώς αποδείξαμε ότι 
 είναι συνεχής στο
είναι συνεχής στο ![\displaystyle{[-3,0]} \displaystyle{[-3,0]}](/forum/ext/geomar/texintegr/latexrender/pictures/73b2441f86c04f56f5aee17d1c791447.png) ως άθροισμα και σύνθεση συνεχών συναρτήσεων.
ως άθροισμα και σύνθεση συνεχών συναρτήσεων. δηλαδή το
δηλαδή το 



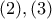 προκύπτει ότι
προκύπτει ότι  άρα η συνάρτηση είναι γνησίως αύξουσα, κατά συνέπεια, το
άρα η συνάρτηση είναι γνησίως αύξουσα, κατά συνέπεια, το 



 έχω
έχω 
 θα έχω:
θα έχω: 

 και προκύπτει
και προκύπτει 

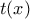 με τον άξονα
με τον άξονα 

![\displaystyle{t(x)\geq 0\Leftrightarrow x\in (-\infty ,0]\cup [2,+\infty )} \displaystyle{t(x)\geq 0\Leftrightarrow x\in (-\infty ,0]\cup [2,+\infty )}](/forum/ext/geomar/texintegr/latexrender/pictures/070d454d3ef30e2936aff82f5a6bed6c.png)
![\displaystyle{t(x)\leq 0\Leftrightarrow x\in [0 ,2]} \displaystyle{t(x)\leq 0\Leftrightarrow x\in [0 ,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/2291727cc246a281c3efe99a90535a70.png) και εφόσον η συνάρτηση
και εφόσον η συνάρτηση  είναι συνεχής, το ζητούμενο εμβαδόν είναι
είναι συνεχής, το ζητούμενο εμβαδόν είναι
![\displaystyle{=4[\frac{x^{2}}{2}]_{0}^{2}-2[\frac{x^{3}}{3}]_{0}^{3}=...=\frac{8}{3}} \displaystyle{=4[\frac{x^{2}}{2}]_{0}^{2}-2[\frac{x^{3}}{3}]_{0}^{3}=...=\frac{8}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/67594498b8d014218a5e2a9e16271bed.png) τ.μ. που είναι και το ζητούμενο εμβαδόν.
τ.μ. που είναι και το ζητούμενο εμβαδόν.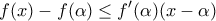 για κάθε
για κάθε ![\displaystyle{x\in [\alpha ,\beta ]} \displaystyle{x\in [\alpha ,\beta ]}](/forum/ext/geomar/texintegr/latexrender/pictures/955a46e44f3dbabeb556a2589544b656.png)
![\displaystyle{[\alpha ,x ]} \displaystyle{[\alpha ,x ]}](/forum/ext/geomar/texintegr/latexrender/pictures/fa3f8807fcdff77e0d36abc66881bc16.png)

 δηλαδή
δηλαδή 
 και εφόσον
και εφόσον  σημαίνει ότι η
σημαίνει ότι η  είναι γνησίως αύξουσα συνάρτηση.
είναι γνησίως αύξουσα συνάρτηση. και επειδή
και επειδή  μπορούμε να πολλαπλασιάσουμε την
μπορούμε να πολλαπλασιάσουμε την  με το
με το  και προκύπτει
και προκύπτει 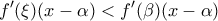
 ) έχουμε ότι
) έχουμε ότι  για κάθε
για κάθε 
![[\alpha, \beta] [\alpha, \beta]](/forum/ext/geomar/texintegr/latexrender/pictures/449a655262b1fd7ada210efdeeea929f.png) , τότε
, τότε 

![\displaystyle{\int_{\alpha }^{\beta }f(x)dx-f(\alpha )(\beta -\alpha )\leq f'(\beta )[\frac{x^{2}}{2}-\alpha x]_{\alpha }^{\beta }\Leftrightarrow \int_{\alpha }^{\beta }f(x)dx-f(\alpha )(\beta -\alpha )\leq f'(\beta )[\frac{\beta ^{2}}{2}-\alpha .\beta +\frac{\alpha ^{2}}{2}]\Leftrightarrow} \displaystyle{\int_{\alpha }^{\beta }f(x)dx-f(\alpha )(\beta -\alpha )\leq f'(\beta )[\frac{x^{2}}{2}-\alpha x]_{\alpha }^{\beta }\Leftrightarrow \int_{\alpha }^{\beta }f(x)dx-f(\alpha )(\beta -\alpha )\leq f'(\beta )[\frac{\beta ^{2}}{2}-\alpha .\beta +\frac{\alpha ^{2}}{2}]\Leftrightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/69097a6ef85b124a2d2bfcd13076e1e6.png)

 και έτσι αποδείξαμε το ζητούμενο.
και έτσι αποδείξαμε το ζητούμενο.
![\displaystyle{\left[\begin{matrix}
\left(\lambda-2\right)x+\left(\lambda+2\right)y\\
\left(\lambda-2\right)x+\left(\lambda-1\right)y
\end{matrix}\right]=\left[\begin{matrix}
\lambda+1\\
\lambda-3
\end{matrix}\right]} \displaystyle{\left[\begin{matrix}
\left(\lambda-2\right)x+\left(\lambda+2\right)y\\
\left(\lambda-2\right)x+\left(\lambda-1\right)y
\end{matrix}\right]=\left[\begin{matrix}
\lambda+1\\
\lambda-3
\end{matrix}\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/24c633bb083b88bef526b590b03dbddb.png)

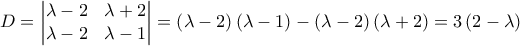
 έχουμε ότι
έχουμε ότι 

![\displaystyle{y=\frac{1}{3\left(2-\lambda\right)}\begin{vmatrix}
\lambda-2 & \lambda+1\\
\lambda-2 & \lambda-3
\end{vmatrix}=\frac{1}{3\left(2-\lambda\right)}\left[\left(\lambda-2\right)\left(\lambda-3\right)-\left(\lambda-2\right)\left(\lambda+1\right)\right]=\frac{4}{3}} \displaystyle{y=\frac{1}{3\left(2-\lambda\right)}\begin{vmatrix}
\lambda-2 & \lambda+1\\
\lambda-2 & \lambda-3
\end{vmatrix}=\frac{1}{3\left(2-\lambda\right)}\left[\left(\lambda-2\right)\left(\lambda-3\right)-\left(\lambda-2\right)\left(\lambda+1\right)\right]=\frac{4}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/02271ddf785d06772832971215107cfa.png)
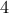 ψήφιους αριθμούς με διαφορετικά ψηφία από
ψήφιους αριθμούς με διαφορετικά ψηφία από  εως
εως 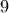 (με το πρώτο ψηφίο να μην είναι
(με το πρώτο ψηφίο να μην είναι  o αριθμός που ψάχνουμε στο δεκαδικό σύστημα
o αριθμός που ψάχνουμε στο δεκαδικό σύστημα έχουμε
έχουμε 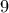 επιλογές,
επιλογές, 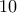 ψηφία που έχουμε δεν μπορεί να μπεί το
ψηφία που έχουμε δεν μπορεί να μπεί το  έχουμε
έχουμε  έχουμε
έχουμε  επιλογές,
επιλογές,  και θέλουμε ένα ψηφίο διαφορετικό από το
και θέλουμε ένα ψηφίο διαφορετικό από το  έχουμε
έχουμε  επιλογές
επιλογές τέτοιοι αριθμοί
τέτοιοι αριθμοί