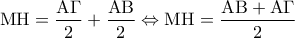Άσκηση: 4762
Στο παρακάτω σχήμα το ορθογώνιο

παριστάνει ένα τραπέζι μπιλιάρδου.
Ένας παίχτης τοποθετεί μια μπάλα στο σημείο

το οποίο ανήκει στη μεσοκάθετη
της

που απέχει από αυτή απόσταση ίση με

. Όταν ο παίχτης χτυπήσει τη
μπάλα αυτή ακολουθεί τη διαδρομή

χτυπώντας στους τοίχους
του μπιλιάρδου

διαδοχικά . Για τη διαδρομή αυτή ισχύει ότι κάθε γωνία
πρόσπτωσης σε τοίχο ( π.χ. η γωνία

) είναι ίση με κάθε γωνία ανάκλασης σε τοίχο (π.χ. η γωνία

) και κάθε μια απ’ αυτές είναι

.
α) Να αποδείξετε ότι :
1. Η διαδρομή

της μπάλας είναι τετράγωνο ( μ 9)
2. Το σημείο

ισαπέχει από τις κορυφές

του μπιλιάρδου. (μ 8)
β) Αν η

είναι διπλάσια από την απόσταση του

από τον τοίχο

να υπολογίσετε τις γωνίες του τριγώνου

. (μ 8)

- 4_4762_εκφώνηση.png (7.16 KiB) Προβλήθηκε 3426 φορές
Σχόλιο:
Στην πιο πάνω άσκηση έχω την εξής άποψη :
Είτε δίδουμε ότι η διαδρομή είναι

και εξ ανάγκης μετά η απόσταση του

, που βρίσκεται στη μεσοκάθετο του

, είναι ίση με

.

- 4_4762_α ερώτημα.png (14.12 KiB) Προβλήθηκε 3426 φορές
Είτε δίδουμε ότι η απόσταση του

από τη

είναι ίση με

και εξ ανάγκης μετά η διαδρομή είναι

.

- 4_4762_α ερώτημα_1.png (15.79 KiB) Προβλήθηκε 3426 φορές
Και τα δύο σαν δεδομένα μόνο σύγχυση μπορούν να προκαλέσουν .
Και στις δύο περιπτώσεις η διαδρομή ορίζει τετράγωνο. Αλλά η άσκηση δεν είναι απλή για τους μαθητές. Εικάζω ότι ο θεματοδότης θέλει να βοηθήσει τα παιδιά
αλλά αυτό έχει αντίθετο αποτέλεσμα ιδίως για του διαβασμένους μαθητές .
 με
με  , εγγεγραμμένο σε κύκλο με κέντρο
, εγγεγραμμένο σε κύκλο με κέντρο  . Θεωρούμε το μέσο
. Θεωρούμε το μέσο  του κυρτογώνιου τόξου
του κυρτογώνιου τόξου  και το ύψος
και το ύψος  του τριγώνου
του τριγώνου  .
.  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας 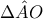 . (Μονάδες 8)
. (Μονάδες 8)  (Μονάδες 9)
(Μονάδες 9) (Μονάδες 8)
(Μονάδες 8)  . Τότε η ευθεία
. Τότε η ευθεία  διέρχεται από το μέσο
διέρχεται από το μέσο  του τόξου
του τόξου 
 απόστημα και
απόστημα και  ύψος:
ύψος:  .
. ως εντός εναλλάξ.
ως εντός εναλλάξ. ως προσκείμενες στη βάση γωνίες ισοσκελούς τριγώνου.
ως προσκείμενες στη βάση γωνίες ισοσκελούς τριγώνου.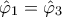 δηλ.
δηλ.  διχοτόμος
διχοτόμος  .
. ως εγγεγραμμένες γωνίες στα ίσα τόξα
ως εγγεγραμμένες γωνίες στα ίσα τόξα  .
. . Αλλά
. Αλλά  , οπότε
, οπότε 
 και
και έχω:
έχω:  και
και  . Έτσι,
. Έτσι, 

 και στην προέκταση της
και στην προέκταση της  θεωρούμε σημείο
θεωρούμε σημείο  τέτοιο ώστε
τέτοιο ώστε 
 τέτοιο ώστε
τέτοιο ώστε  .
.  .
.  είναι συνευθειακά.
είναι συνευθειακά.  (ως εντός εκτός και επί τα αυτά μέρη των παραλλήλων
(ως εντός εκτός και επί τα αυτά μέρη των παραλλήλων  και
και  που τέμνονται από τη
που τέμνονται από τη  και
και  (ως εντός εναλλάξ των παραλλήλων
(ως εντός εναλλάξ των παραλλήλων  ).
).  (ως άθροισμα των γωνιών του τριγώνου
(ως άθροισμα των γωνιών του τριγώνου  ). Άρα
). Άρα  .
.  ως παραπληρωματικές των ίσων γωνιών
ως παραπληρωματικές των ίσων γωνιών  αντίστοιχα του παραλληλογράμμου.
αντίστοιχα του παραλληλογράμμου. και
και  έχουν τις γωνίες των κορυφών τους ίσες, οπότε τα είναι και οι γωνίες των βάσεων ίσες, δηλαδή
έχουν τις γωνίες των κορυφών τους ίσες, οπότε τα είναι και οι γωνίες των βάσεων ίσες, δηλαδή  ως εντός και εναλλάξ.
ως εντός και εναλλάξ.

 ευθεία, πράγμα το οποίο ζητείται να αποδειχθεί.
ευθεία, πράγμα το οποίο ζητείται να αποδειχθεί. έγινε
έγινε  . Ευχαριστώ τον προσωπικό μου διορθωτή Γιάννη (παρακάτω) που το πρόσεξε
. Ευχαριστώ τον προσωπικό μου διορθωτή Γιάννη (παρακάτω) που το πρόσεξε υπάρχει σφάλμα.
υπάρχει σφάλμα. με γωνία
με γωνία  ορθή. Φέρνουμε τη διάμεσο
ορθή. Φέρνουμε τη διάμεσο  την κάθετη στην
την κάθετη στην  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Αν
αντίστοιχα. Αν  να αποδείξετε ότι:
να αποδείξετε ότι: (Μονάδες
(Μονάδες  )
) (Μονάδες
(Μονάδες  )
) τέμνει κάθετα τη
τέμνει κάθετα τη  (Μονάδες
(Μονάδες  και κατά συνέπεια
και κατά συνέπεια 
 , οπότε
, οπότε 

 \displaystyle{\displaystyle{ \Leftrightarrow {\rm M}\widehat {\rm A}{\rm B} = \frac{{{\rm A}\widehat {\rm M}\Gamma }}{2}}
\displaystyle{\displaystyle{ \Leftrightarrow {\rm M}\widehat {\rm A}{\rm B} = \frac{{{\rm A}\widehat {\rm M}\Gamma }}{2}} (1)
(1)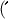 AMB
AMB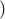 \displaystyle{{\rm K}\widehat {\rm H}{\rm Z} = \Delta \widehat {\rm H}{\rm A} = {180^0} - 2{\rm A}\widehat \Delta {\rm H}}}
\displaystyle{{\rm K}\widehat {\rm H}{\rm Z} = \Delta \widehat {\rm H}{\rm A} = {180^0} - 2{\rm A}\widehat \Delta {\rm H}}}
 (από το ισοσκελές τρίγωνο
(από το ισοσκελές τρίγωνο  .
. έχουμε:
έχουμε: 
 , οπότε το τετράπλευρο
, οπότε το τετράπλευρο  είναι εγγράψιμο (μία γωνία του είναι ίση με την
είναι εγγράψιμο (μία γωνία του είναι ίση με την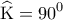 , θα είναι και
, θα είναι και 
 και
και  με
με  ,
,  και
και  ,
, 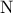 τα μέσα των
τα μέσα των  και
και  αντίστοιχα.
αντίστοιχα.  . (Μονάδες 10)
. (Μονάδες 10)  είναι κάθετη στην
είναι κάθετη στην  . (Μονάδες 10)
. (Μονάδες 10)  (Μονάδες 5)
(Μονάδες 5)  είναι εγγράψιμο σε κύκλο αφού η πλευρά
είναι εγγράψιμο σε κύκλο αφού η πλευρά  , το κέντρο του κύκλου είναι το μέσον
, το κέντρο του κύκλου είναι το μέσον  της
της  . Κατά συνέπεια
. Κατά συνέπεια  ως ακτίνες του κύκλου .
ως ακτίνες του κύκλου .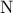 είναι πλέον μέσο χορδής , το
είναι πλέον μέσο χορδής , το 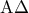 .
.  διότι είναι εγγεγραμμένες και βαίνουν στο ίδιο τόξο .
διότι είναι εγγεγραμμένες και βαίνουν στο ίδιο τόξο . , με διάμετρο
, με διάμετρο  του κύκλου φέρουμε την εφαπτομένη
του κύκλου φέρουμε την εφαπτομένη  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  φέρουμε τα τμήματα
φέρουμε τα τμήματα  κάθετα στην ευθεία
κάθετα στην ευθεία  και
και  είναι διχοτόμοι των γωνιών
είναι διχοτόμοι των γωνιών  και
και  αντίστοιχα. (Μονάδες 8)
αντίστοιχα. (Μονάδες 8) είναι ύψος του τριγώνου
είναι ύψος του τριγώνου  , να αποδείξετε ότι
, να αποδείξετε ότι  . (Μονάδες 8)
. (Μονάδες 8) . (Μονάδες 9)
. (Μονάδες 9) ως γωνία χορδής – εφαπτομένης και :
ως γωνία χορδής – εφαπτομένης και :
 ,οπότε η
,οπότε η  .
. είναι τραπέζιο αφού
είναι τραπέζιο αφού  ως κάθετες στην ίδια ευθεία .
ως κάθετες στην ίδια ευθεία . ,οπότε
,οπότε  κι αφού το
κι αφού το  είναι μέσον της
είναι μέσον της  , η
, η  είναι διάμεσος του τραπεζίου . Επομένως
είναι διάμεσος του τραπεζίου . Επομένως 

 , έχουμε
, έχουμε 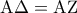 και τελικά
και τελικά 
 είναι η διάμεσος του τραπεζίου και ισχύει :
είναι η διάμεσος του τραπεζίου και ισχύει :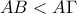 . Από το
. Από το  φέρουμε κάθετη στην διχοτόμο
φέρουμε κάθετη στην διχοτόμο , η οποία τέμνει την
, η οποία τέμνει την  και έστω
και έστω 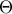 το μέσο της πλευράς
το μέσο της πλευράς  .
. είναι ρόμβος. (Μονάδες 9)
είναι ρόμβος. (Μονάδες 9) είναι τραπέζιο. (Μονάδες 9)
είναι τραπέζιο. (Μονάδες 9)  . (Μονάδες 7)
. (Μονάδες 7)
 το
το  .
. ,
,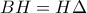 .
.  ,
, ρόμβος.
ρόμβος. και
και  (1).
(1). , τα
, τα  (2). Λόγω των (1) και (2),
(2). Λόγω των (1) και (2), 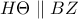 .
.
 τότε
τότε 

 τότε
τότε  με
με  και
και  .Αν
.Αν  τα μέσα των διαγωνίων
τα μέσα των διαγωνίων  αντίστοιχα και αν οι πλευρές
αντίστοιχα και αν οι πλευρές  προεκτεινόμενες τέμνονται κάθετα στο
προεκτεινόμενες τέμνονται κάθετα στο  να αποδειχθεί ότι:
να αποδειχθεί ότι: είναι παραλληλόγραμμο;Αιτιολογήστε την απάντησή σας.
είναι παραλληλόγραμμο;Αιτιολογήστε την απάντησή σας. ως εντός εναλλάξ.Επομένως στο ορθογώνιο τρίγωνο
ως εντός εναλλάξ.Επομένως στο ορθογώνιο τρίγωνο  η πλευρά
η πλευρά  βρίσκεται απέναντι από γωνία
βρίσκεται απέναντι από γωνία  κι έτσι είναι ίση με το μισό
κι έτσι είναι ίση με το μισό  .
. .
. η πλευρά
η πλευρά  βρίσκεται απέναντι από γωνία
βρίσκεται απέναντι από γωνία  .
.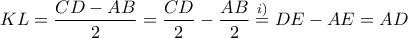 όπως θέλαμε.
όπως θέλαμε.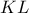 γνωρίζουμε ότι είναι παράλληλη στην
γνωρίζουμε ότι είναι παράλληλη στην  .
.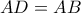 .
. είναι το σημείο
είναι το σημείο  και από το μέσο της
και από το μέσο της  της
της  φέρνουμε τμήματα
φέρνουμε τμήματα  ίσο και παράλληλο με το
ίσο και παράλληλο με το  και
και  ίσο και παράλληλο με το
ίσο και παράλληλο με το 
 βρίσκονται στο ίδιο ημιεπίπεδο της
βρίσκονται στο ίδιο ημιεπίπεδο της  ).
). είναι συνευθειακά.
είναι συνευθειακά. ισούται με την περίμετρο του τριγώνου
ισούται με την περίμετρο του τριγώνου  είναι παραλληλόγραμμο αφού
είναι παραλληλόγραμμο αφού 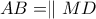 επομένως
επομένως  .
. είναι παραλληλόγραμμο κι έτσι
είναι παραλληλόγραμμο κι έτσι  .
. .Ακόμη
.Ακόμη  λόγω των παραλληλογράμμων
λόγω των παραλληλογράμμων  .
. είναι ίσα άρα έχουν και ίσες περιμέτρους.
είναι ίσα άρα έχουν και ίσες περιμέτρους. με τη γωνία
με τη γωνία  και
και  οι οποίες τέμνουν τις
οι οποίες τέμνουν τις  είναι ορθή.
είναι ορθή. .
.
 και
και 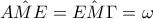
 άρα
άρα 
 είναι διάμεσος του ορθογωνίου τριγώνου
είναι διάμεσος του ορθογωνίου τριγώνου  που αντιστοιχεί στην υποτείνουσα άρα
που αντιστοιχεί στην υποτείνουσα άρα 
 είναι διάμεσος του ορθογωνίου τριγώνου
είναι διάμεσος του ορθογωνίου τριγώνου  που αντιστοιχεί στην υποτείνουσα άρα
που αντιστοιχεί στην υποτείνουσα άρα 

 ως εντός εναλλάξ των παραλλήλων
ως εντός εναλλάξ των παραλλήλων  με τέμνουσα την
με τέμνουσα την  . Επίσης
. Επίσης  αφού
αφού  . Συνεπώς το τρίγωνο
. Συνεπώς το τρίγωνο  είναι ισοσκελές και άρα
είναι ισοσκελές και άρα 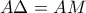 (1)
(1) άρα το τρίγωνο
άρα το τρίγωνο  ισοσκελές και άρα
ισοσκελές και άρα  (2)
(2) (3) ως εντός εναλλάξ των παραλλήλων
(3) ως εντός εναλλάξ των παραλλήλων  . Από (2),(3) είναι
. Από (2),(3) είναι  άρα
άρα 
 παριστάνει ένα τραπέζι μπιλιάρδου.
παριστάνει ένα τραπέζι μπιλιάρδου. το οποίο ανήκει στη μεσοκάθετη
το οποίο ανήκει στη μεσοκάθετη  που απέχει από αυτή απόσταση ίση με
που απέχει από αυτή απόσταση ίση με  χτυπώντας στους τοίχους
χτυπώντας στους τοίχους διαδοχικά . Για τη διαδρομή αυτή ισχύει ότι κάθε γωνία
διαδοχικά . Για τη διαδρομή αυτή ισχύει ότι κάθε γωνία  ) είναι ίση με κάθε γωνία ανάκλασης σε τοίχο (π.χ. η γωνία
) είναι ίση με κάθε γωνία ανάκλασης σε τοίχο (π.χ. η γωνία  ) και κάθε μια απ’ αυτές είναι
) και κάθε μια απ’ αυτές είναι  .
. του μπιλιάρδου. (μ 8)
του μπιλιάρδου. (μ 8) είναι διπλάσια από την απόσταση του
είναι διπλάσια από την απόσταση του  να υπολογίσετε τις γωνίες του τριγώνου
να υπολογίσετε τις γωνίες του τριγώνου  . (μ 8)
. (μ 8)
 με τη γωνία
με τη γωνία  φέρουμε
φέρουμε 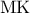 κάθετη στην
κάθετη στην 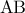 και
και  κάθετη στην
κάθετη στην  .
.  είναι τα μέσα των
είναι τα μέσα των  και
και 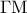 αντίστοιχα, να αποδείξετε ότι:
αντίστοιχα, να αποδείξετε ότι: 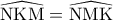
 .
. 
 ως διάμεσος στην υποτείνουσα
ως διάμεσος στην υποτείνουσα  του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου  .
. είναι ισοσκελές δηλαδή
είναι ισοσκελές δηλαδή  ως διάμεσος στην υποτείνουσα
ως διάμεσος στην υποτείνουσα  το
το  ως διάμεσος στην υποτείνουσα
ως διάμεσος στην υποτείνουσα  του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου 

 σειρά πριν από την παρένθεση, η σχέση:
σειρά πριν από την παρένθεση, η σχέση:  (εντός εναλλάξ...)
(εντός εναλλάξ...) σειρά πρέπει να γραφεί:
σειρά πρέπει να γραφεί: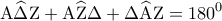 (άθροισμα γωνιών...)
(άθροισμα γωνιών...) και εντός αυτού ισόπλευρο τρίγωνο
και εντός αυτού ισόπλευρο τρίγωνο  . Αν η προέκταση της
. Αν η προέκταση της  (Μονάδες
(Μονάδες  και
και  είναι ίσα. (Μονάδες
είναι ίσα. (Μονάδες  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  (Μονάδες
(Μονάδες  και
και  .
. .
.

 (πλευρές τετραγώνου) και
(πλευρές τετραγώνου) και  (η διαγώνιος τετραγώνου διχοτομεί τις γωνίες του).
(η διαγώνιος τετραγώνου διχοτομεί τις γωνίες του).
 , θα είναι και
, θα είναι και  , δηλαδή η
, δηλαδή η  και σημείο
και σημείο  κάθετη στην
κάθετη στην  φέρουμε
φέρουμε 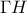 κάθετη στην
κάθετη στην  κάθετη στην
κάθετη στην  .
.  είναι ίση με τη γωνία
είναι ίση με τη γωνία  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας . (Μονάδες 4)
. (Μονάδες 4)  είναι ισοσκελές. (Μονάδες 9)
είναι ισοσκελές. (Μονάδες 9)  (Μονάδες 8)
(Μονάδες 8)
 άρα το
άρα το  είναι ορθογώνιο αφού έχει 3 ορθές γωνίες. Άρα
είναι ορθογώνιο αφού έχει 3 ορθές γωνίες. Άρα
 άρα
άρα  ως εντός εκτός και επί τα αυτά μέρη των
ως εντός εκτός και επί τα αυτά μέρη των που τέμνονται από την
που τέμνονται από την  ως κατά κορυφήν
ως κατά κορυφήν 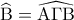 αφού το
αφού το  από ερώτημα (α).
από ερώτημα (α).  \displaystyle{\Rightarrow}
\displaystyle{\Rightarrow} άρα
άρα  και έχουμε ότι η
και έχουμε ότι η  διχοτόμος της
διχοτόμος της 
 αυτά έχουν:
αυτά έχουν: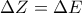 άρα το τρίγωνο
άρα το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές.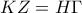 (1) (απέναντι πλευρές ορθογωνίου)
(1) (απέναντι πλευρές ορθογωνίου)
 \displaystyle{\Delta K=\Delta E+H\Gamma}
\displaystyle{\Delta K=\Delta E+H\Gamma}

 αντίστοιχα η εσωτερική και η εξωτερική διχοτόμος της γωνίας
αντίστοιχα η εσωτερική και η εξωτερική διχοτόμος της γωνίας  σημεία της ευθείας
σημεία της ευθείας  κάθετη στην
κάθετη στην  κάθετη στην
κάθετη στην  είναι ορθογώνιο.
είναι ορθογώνιο.  είναι ίση με τη γωνία
είναι ίση με τη γωνία  .
.  διέρχεται από το
διέρχεται από το 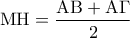
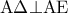 ως διχοτόμοι εφεξής και παραπληρωματικών γωνιών.
ως διχοτόμοι εφεξής και παραπληρωματικών γωνιών. είναι το κέντρο του
είναι το κέντρο του  ως μισά των ίσων διαγωνίων
ως μισά των ίσων διαγωνίων 
 είναι ισοσκελές δηλαδή
είναι ισοσκελές δηλαδή 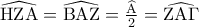 .
.
 δηλαδή η
δηλαδή η  είναι παράλληλη στην
είναι παράλληλη στην