 , που ικανοποιούν την
, που ικανοποιούν την 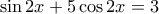 .
.Πρόβλημα 2: Να λύσετε την ανίσωση
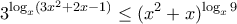
Πρόβλημα 3: Να βρείτε όλες τις δυνατές τιμές του αθροίσματος της φθίνουσας αριθμητικής προόδου
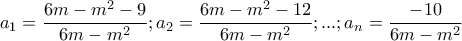
όπου
 τυχαίος ακέραιος.
τυχαίος ακέραιος.Πρόβλημα 4: Στο κυρτό τετράπλευρο
 οι διαγώνιοι
οι διαγώνιοι 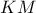 και
και 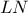 είναι κάθετες στις πλευρές
είναι κάθετες στις πλευρές  και
και  αντίστοιχα και το μήκος της πλευράς
αντίστοιχα και το μήκος της πλευράς  είναι ίσο με
είναι ίσο με 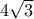 . Στην πλευρά
. Στην πλευρά  βρίσκεται σημείο
βρίσκεται σημείο  τέτοιο ώστε
τέτοιο ώστε  . Είναι γνωστό ότι
. Είναι γνωστό ότι  . Να βρείτε το μήκος της τεθλασμένης
. Να βρείτε το μήκος της τεθλασμένης 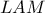 και το εμβαδόν του τετραπλεύρου
και το εμβαδόν του τετραπλεύρου  , αν
, αν 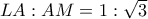 .
.Πρόβλημα 5: Να βρείτε όλες τις τιμές της παραμέτρου
 , για τις οποίες η εξίσωση
, για τις οποίες η εξίσωση
έχει ακριβώς τρεις λύσεις.
Πρόβλημα 6: Δίνεται σφαίρα ακτίνας 1 και κέντρου
 . Από σημείο
. Από σημείο  εκτός σφαίρας φέρουμε τέσσερεις ευθείες. Η πρώτη ευθεία τέμνει την επιφάνεια της σφαίρα κατα σειρά στα σημεία
εκτός σφαίρας φέρουμε τέσσερεις ευθείες. Η πρώτη ευθεία τέμνει την επιφάνεια της σφαίρα κατα σειρά στα σημεία  και
και  , η δεύτερη στα σημεία
, η δεύτερη στα σημεία 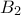 και
και 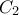 , η τρίτη στα σημεία
, η τρίτη στα σημεία 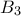 και
και  , η τέταρτη στα σημεία
, η τέταρτη στα σημεία  και
και 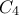 . Οι ευθείες
. Οι ευθείες 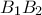 και
και 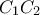 τέμνονται στο σημείο
τέμνονται στο σημείο  και οι ευθείες
και οι ευθείες 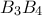 και
και 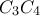 στο σημείο
στο σημείο  . Να βρείτε τον όγκο της πυραμίδας
. Να βρείτε τον όγκο της πυραμίδας  , αν
, αν  ,
,  και η γωνία μεταξύ των εδρών
και η γωνία μεταξύ των εδρών 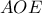 και
και  είναι ίση με
είναι ίση με 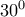 .
.
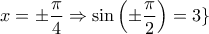 απορρίπτεται λοιπόν.
απορρίπτεται λοιπόν.



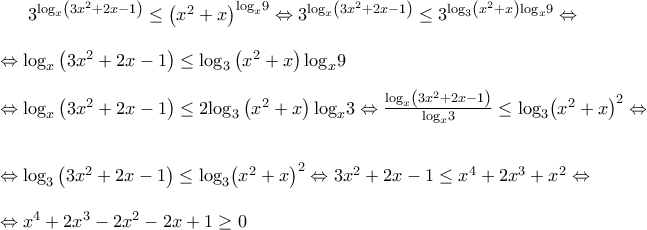

![\displaystyle { x \in (\frac{1}{3}, \sqrt{2} -1] \cup (1 , + \infty) } \displaystyle { x \in (\frac{1}{3}, \sqrt{2} -1] \cup (1 , + \infty) }](/forum/ext/geomar/texintegr/latexrender/pictures/8c89f790db83923430df8b3564944316.png)
 , οπότε
, οπότε  . Επίσης, αφού
. Επίσης, αφού  έχουμε μόνο
έχουμε μόνο 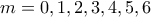 . Κρατάμε εκείνα τα
. Κρατάμε εκείνα τα  , δηλαδή τα
, δηλαδή τα  με αντίστοιχα
με αντίστοιχα 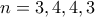 . Τώρα η άσκηση έγινε τετριμμένη (άμεσος έλεγχος τεσσάρων απλών περιπτώσεων).
. Τώρα η άσκηση έγινε τετριμμένη (άμεσος έλεγχος τεσσάρων απλών περιπτώσεων). είναι διαφορετικά μεταξύ τους. Είναι μεν απλό, αλλά απαραίτητο.
είναι διαφορετικά μεταξύ τους. Είναι μεν απλό, αλλά απαραίτητο. της
της  , τότε παρατηρούμε πως η
, τότε παρατηρούμε πως η  είναι ρίζα και της
είναι ρίζα και της 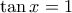 και της
και της  . Στο άθροισμα όμως πρέπει να την μετρήσουμε μία φορά.
. Στο άθροισμα όμως πρέπει να την μετρήσουμε μία φορά.