ΕΜΠ 1961 ΑΛΓΕΒΡΑ ΠΟΛ. ΜΗΧ.

parmenides51 · #1

Εξεταστής Φ.Βασιλείου

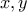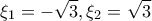1. α) Θεωρούμε πολυώνυμο $\displaystyle{f(x,y)}$ δυο αγνώστων $\displaystyle{x,y}$ με συντελεστές ακεραίους αριθμούς, τέτοιο ώστε η εξίσωση $\displaystyle{f(x,y)=0}$ να επαληθεύεται από το ζεύγος $\displaystyle{ \xi_1=-\sqrt3, \xi_2=\sqrt3}$ των ριζών της εξίσωσης $\displaystyle{g(x)=x^2-3=0}$ . Να δείξετε οτι το πολυώνυμο $\displaystyle{f(x,-x)}$ του ενός αγνώστου $\displaystyle{x}$ , το οποίο προκύπτει από το $\displaystyle{f(x,y)}$ με την αντικατάσταση του $\displaystyle{y}$ από το $\displaystyle{-x}$ , διαιρείται από το $\displaystyle{g(x)}$ , οτι δηλαδή στην σχέση $\displaystyle{ f(x,-x)=g(x)\pi(x)+\upsilon (x)}$ , όπου $\displaystyle{ \pi(x) }$ είναι το πηλίκο και $\displaystyle{\upsilon (x)}$ το υπόλοιπο της διαίρεσης του $\displaystyle{ f(x,-x)}$ με το $\displaystyle{g(x)}$ , το $\displaystyle{\upsilon (x) }$ είναι ταυτοτικά ίσο με $\displaystyle{0}$ . Να συμπεράνετε τότε από αυτό, οτι το ζεύγος $\displaystyle{\xi_2,\xi_1}$ επαληθεύει την εξίσωση $\displaystyle{ f(x,y)=0}$ .
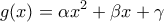β) Με ποιο διώνυμο του x αν αντικατασταθεί το $\displaystyle{y}$ στο $\displaystyle{f(x,y)}$ ισχύει γενικώς η πρόταση για $\displaystyle{g(x)=\alpha x^2+\beta x+\gamma}$ , όταν οι συντελεστές 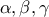$\displaystyle{\alpha,\beta,\gamma}$ είναι ακέραιοι, το $\displaystyle{\beta^2-4\alpha \gamma}$ είναι θετικό και δεν είναι τετράγωνο ακεραίου.
γ) Αντίθετα για $\displaystyle{g(x)=x^2-4}$ , να δείξετε με ένα παράδειγμα, παίρνοντας κατάλληλο $\displaystyle{f(x,y)}$ ότι στην παραπάνω σχέση διαίρεσης το $\displaystyle{ \upsilon (x)}$ μπορεί να μην είναι ταυτοτικά $\displaystyle{0}$ .

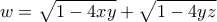2. α) Να δείξετε οτι εαν οι πραγματικοί αριθμοί $\displaystyle{x,y,z}$ δεν είναι και οι τρεις ίσοι μεταξύ τους και τα υπόρριζα τους δεύτερου μέλους της παράστασης $\displaystyle{ w=\sqrt{1-4xy}+\sqrt{1-4yz}}$ είναι μεγαλύτερα ή ίσα του μηδενός, τότε από την σχέση $\displaystyle{w\ge 4y}$ έπεται οτι τουλάχιστον ένας από τους $\displaystyle{x,y,z}$ είναι μικρότερος του $\displaystyle{\frac{1}{\sqrt8}}$ .
β) Τι ονομάζεται βαθμός πολυωνύμου του $\displaystyle{x}$ ; Ποια πολυώνυμα είναι μηδενικού βαθμού; Μιλάμε για βαθμό για τα ταυτοτικά ίσα με το $\displaystyle{0}$ πολυώνυμα και γιατί;

3. α) Πως η επίλυση μια διοφαντικής εξίσωσης με τρεις αγνώστους μπορεί να αναχθεί στην επίλυση περισσοτέρων διοφαντικών εξισώσεων με δυο αγνώστους;
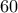β) Να βρείτε σαν εφαρμογή όλες τις περιπτώσεις κατά τις οποίες μπορεί κάποιος να αγοράσει με ποσό ακριβώς $\displaystyle{600}$ δρχ. ταινίες μαγνητοφώνου, από τρια τέτοια είδη, αξίας κάθε ταινίας του πρώτου είδους $\displaystyle{60}$ , του δευτέρου $\displaystyle{72}$ και του τρίτου $\displaystyle{90}$ δραχμών.

Ορέστης Λιγνός · #2

parmenides51 έγραψε:2. α) Να δείξετε οτι εαν οι πραγματικοί αριθμοί $\displaystyle{x,y,z}$ δεν είναι και οι τρεις ίσοι μεταξύ τους και τα υπόρριζα τους δεύτερου μέλους της παράστασης $\displaystyle{ w=\sqrt{1-4xy}+\sqrt{1-4yz}}$ είναι μεγαλύτερα ή ίσα του μηδενός, τότε από την σχέση $\displaystyle{w\ge 4y}$ έπεται οτι τουλάχιστον ένας από τους $\displaystyle{x,y,z}$ είναι μικρότερος του $\displaystyle{\frac{1}{\sqrt8}}$ .

Καλησπέρα!

Αν υποθέταμε ότι $x,y,z > \dfrac{1}{\sqrt{8}}$ , τότε, θα είχαμε $xy>\dfrac{1}{8},yz>\dfrac{1}{8}$

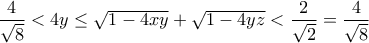$\dfrac{4}{\sqrt{8}}<4y \leq \sqrt{1-4xy}+\sqrt{1-4yz} < \dfrac{2}{\sqrt{2}}=\dfrac{4}{\sqrt{8}}$ , που είναι προφανώς αδύνατο.

Συνεπώς, ένας τουλάχιστον εκ των x,y,z

είναι $\leq \dfrac{1}{8}$ .

ΕΜΠ 1961 ΑΛΓΕΒΡΑ ΠΟΛ. ΜΗΧ.

ΕΜΠ 1961 ΑΛΓΕΒΡΑ ΠΟΛ. ΜΗΧ.

Re: ΕΜΠ 1961 ΑΛΓΕΒΡΑ ΠΟΛ. ΜΗΧ.

Μέλη σε σύνδεση