Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
-
Επιτροπή Θεμάτων 2023
- Δημοσιεύσεις: 28
- Εγγραφή: Πέμ Μάιος 12, 2016 9:41 am
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Αγαπητές/τοί
αναρτούμε την 1η έκδοση των λύσεων των θεμάτων Μαθηματικών προασνατολισμού 2017
η οποία είναι αποτέλεσμα συλλογικής δουλειάς των Επιμελητών του mathematica.gr.
Θέματα & Λύσεις Μαθηματικών προσαν. 2017 (2η έκδοση)
edit: 13/6/2017 ανανεώθηκε ο σύνδεσμος.
αναρτούμε την 1η έκδοση των λύσεων των θεμάτων Μαθηματικών προασνατολισμού 2017
η οποία είναι αποτέλεσμα συλλογικής δουλειάς των Επιμελητών του mathematica.gr.
Θέματα & Λύσεις Μαθηματικών προσαν. 2017 (2η έκδοση)
edit: 13/6/2017 ανανεώθηκε ο σύνδεσμος.
Λέξεις Κλειδιά:
- Λάμπρος Μπαλός
- Δημοσιεύσεις: 984
- Εγγραφή: Τρί Αύγ 13, 2013 12:21 pm
- Τοποθεσία: Τρίκαλα
Re: Μαθηματικά προσανατολισμού 2017
Βεβαίως. Πολύ καλή απάντηση επίσης, που συνάντησα, ήταν η εξής :epep έγραψε:Για τη δικαιολόγηση του Ψ στο Α2 θεωρώ ότι είναι αρκετή η αναφορά (χωρίς απόδειξη) στη συνάρτησηή ακόμα και στην
, αφού και οι δύο αναφέρονται στη θεωρία του σχολικού βιβλίου ως συνεχείς και μη παραγωγίσιμες στο 0.
"παράδειγμα αποτελεί η συνάρτηση του Δ Θέματος όπου και αποδεικνύεται ότι είναι συνεχής στο
 αλλά όχι παραγωγίσιμη".
αλλά όχι παραγωγίσιμη".Λάμπρος Μπαλός
lamprosbalos81@gmail.com
lamprosbalos81@gmail.com
-
Μιχάλης Τσουρακάκης
- Δημοσιεύσεις: 2770
- Εγγραφή: Παρ Ιαν 11, 2013 4:17 am
- Τοποθεσία: Ηράκλειο Κρήτης
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
διαγράφεται λόγω μιας αβλεψίας
τελευταία επεξεργασία από Μιχάλης Τσουρακάκης σε Σάβ Ιουν 10, 2017 1:05 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Δεν καταλαβαίνω.ΣυγκεκριμέναΜιχάλης Τσουρακάκης έγραψε:Mια λύση τουανεξάρτητη των προηγούμενων ερωτημάτων
Θεωρούμε την συνάρτησημε
που είναι παραγωγίσιμη στο
Για κάθεείναι
γνήσια φθίνουσα στο
Άρακαι για
είναι
Επειδή όμως ηδεν μηδενίζεται παντού στο
θα είναι τελικά

Αν καταλαβαίνω καλά
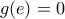 . Aπό που προκύπτει;
. Aπό που προκύπτει;-
Μιχάλης Τσουρακάκης
- Δημοσιεύσεις: 2770
- Εγγραφή: Παρ Ιαν 11, 2013 4:17 am
- Τοποθεσία: Ηράκλειο Κρήτης
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Πολύ σωστά.Από αβλεψία θεώρησα g(e)=0ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Δεν καταλαβαίνω.ΣυγκεκριμέναΜιχάλης Τσουρακάκης έγραψε:Mια λύση τουανεξάρτητη των προηγούμενων ερωτημάτων
Θεωρούμε την συνάρτησημε
που είναι παραγωγίσιμη στο
Για κάθεείναι
γνήσια φθίνουσα στο
Άρακαι για
είναι
Επειδή όμως ηδεν μηδενίζεται παντού στο
θα είναι τελικά
Αν καταλαβαίνω καλά. Aπό που προκύπτει;
Διαγράφεται.Ευχαριστώ για την επισήμανση.Εξ άλλου δεν έχει νόημα
 και
και 
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Στο 2ο δελτίο θεμάτων με τις απαντήσεις που ανέβηκε λείπει το πεδίο τιμών της f στο Β1 ερώτημα
Γιατί πάντα αριθμόν έχοντι. Άνευ τούτου ουδέν νοητόν και γνωστόν.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Δεν έχω δει την επίσημη λύση της Γ1, αλλά κοίταξα διάφορες εδώ και εκεί. Γράφω άλλη μία κάπως πιο απλή αλλά στο ίδιο μήκος κύματος με τρεις στο δικό μας φόρουμ (η τέταρτη, του Παντελή Μιντεκίδη, είναι διαφορετική αλλά αρκετά αφύσικη και άκομψη).
Για να δείξουμε ότι δεν υπάρχουν άλλες εφαπτόμενες που διέρχονται από το πέρα από αυτές στα
πέρα από αυτές στα  , έστω
, έστω  . Η εφαπτομένη στο
. Η εφαπτομένη στο 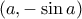 έχει κλίση
έχει κλίση  . Επίσης θα έπρεπε να έχει κλίση
. Επίσης θα έπρεπε να έχει κλίση
 , που αντιβαίνει στην
, που αντιβαίνει στην  . Όμοια έχουμε άτοπο για τα υπόλοιπα
. Όμοια έχουμε άτοπο για τα υπόλοιπα  ή, εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξονα
ή, εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξονα  .
.
Σχολιάζω/προβλέπω ότι το ερώτημα Γ1 θα έχει σχεδόν καθολική αποτυχία στα γραπτά των υποψηφίων. Ίδωμεν.
Για να δείξουμε ότι δεν υπάρχουν άλλες εφαπτόμενες που διέρχονται από το
 πέρα από αυτές στα
πέρα από αυτές στα  , έστω
, έστω  . Η εφαπτομένη στο
. Η εφαπτομένη στο 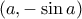 έχει κλίση
έχει κλίση  . Επίσης θα έπρεπε να έχει κλίση
. Επίσης θα έπρεπε να έχει κλίση  , που αντιβαίνει στην
, που αντιβαίνει στην  . Όμοια έχουμε άτοπο για τα υπόλοιπα
. Όμοια έχουμε άτοπο για τα υπόλοιπα  ή, εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξονα
ή, εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξονα  .
.Σχολιάζω/προβλέπω ότι το ερώτημα Γ1 θα έχει σχεδόν καθολική αποτυχία στα γραπτά των υποψηφίων. Ίδωμεν.
-
Παντελής Μιντεκίδης
- Δημοσιεύσεις: 15
- Εγγραφή: Τετ Μάιος 29, 2013 11:40 pm
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Αγαπητέ κύριε Μιχάλη Λάμπρου,Mihalis_Lambrou έγραψε:Δεν έχω δει την επίσημη λύση της Γ1, αλλά κοίταξα διάφορες εδώ και εκεί. Γράφω άλλη μία κάπως πιο απλή αλλά στο ίδιο μήκος κύματος με τρεις στο δικό μας φόρουμ (η τέταρτη, του Παντελή Μιντεκίδη, είναι διαφορετική αλλά αρκετά αφύσικη και άκομψη).
Για να δείξουμε ότι δεν υπάρχουν άλλες εφαπτόμενες που διέρχονται από τοπέρα από αυτές στα
, έστω
. Η εφαπτομένη στο
έχει κλίση
. Επίσης θα έπρεπε να έχει κλίση
, που αντιβαίνει στην
. Όμοια έχουμε άτοπο για τα υπόλοιπα
ή, εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξονα
.
Σχολιάζω/προβλέπω ότι το ερώτημα Γ1 θα έχει σχεδόν καθολική αποτυχία στα γραπτά των υποψηφίων. Ίδωμεν.
Ευχαριστώ που κάνατε τον κόπο να ασχοληθείτε με τις λύσεις μου.
1) Εφόσον η δική μου λύση πιστεύετε ότι είναι "αρκετά αφύσικη και άκομψη", δεν μπορεί παρά επίσης να πιστεύετε ότι η δική σας λύση είναι τουλάχιστον αρκετά φυσική και κομψή.
2) Επιτρέψτε μου να μήν σχολιάσω την δική σας λύση, εκτός και αν μου το ζητήσετε.
3) Η λύση μου είναι τόσο αφύσικη και άκομψη όσο αφύσικο και άκομψο είναι το θεώρημα του Rolle, διότι τίποτε άλλο δεν χρησιμοποιεί.
4) Παρακαλώ, ρίξτε μιά ματιά στις ασκήσεις του σχολικού βιβλίου που αφορούν στο θεώρημα Rolle. Οι ασκήσεις Β3(i), B3(ii) εφαρμόζουν αυτήν την μέθοδο. Αλλά παρακάτω η άσκηση Β7 είναι ακριβώς αυτό που κάνω, σχεδόν αυτολεξεί.
Θερμούς χαιρετισμούς,
Παντελής Μιντεκίδης
- Christos.N
- Δημοσιεύσεις: 2105
- Εγγραφή: Πέμ Νοέμ 26, 2009 2:28 pm
- Τοποθεσία: Ίλιον
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Το είπα απο μέσα μου " να τι πρέπει να κάνει ένας άνθρωπος που αντιλαμβάνεται τις τριγωνομετρικές συναρτήσεις αλλά δεν θυμάται ή δεν έχει εμπιστοσύνη στην μνήμη του όταν λύνει εξισώσεις".
Το ίδιο σχήμα βοηθάει να βγάλει κανείς συμπεράσματα για το πρόσημο της παραγώγου.
Υ.Γ. Έχω σχεδιάσει την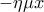 αλλά στο ταμπελάκι έχω τυπογραφικό λάθος.
αλλά στο ταμπελάκι έχω τυπογραφικό λάθος.
Το ίδιο σχήμα βοηθάει να βγάλει κανείς συμπεράσματα για το πρόσημο της παραγώγου.
Υ.Γ. Έχω σχεδιάσει την
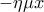 αλλά στο ταμπελάκι έχω τυπογραφικό λάθος.
αλλά στο ταμπελάκι έχω τυπογραφικό λάθος.Χρήστος Ντάβας
Wir müssen wissen — wir werden wissen! D.Hilbert
Wir müssen wissen — wir werden wissen! D.Hilbert
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Το παραπάνω είναι βέβαια ρητορικό επιχείρημα: Το να ισχυριστούμε ότι κάθε λύση που χρησιμοποιεί ένα κομψό Θεώρημα είναι αυτόματα και η ίδια κομψή είναι σαν να λέμε ότι αν κρατάω ένα βιολί Stradivarius αυτόματα η μουσική που θα παίξω είναι αγγελική μελωδία.Παντελής Μιντεκίδης έγραψε: 3) Η λύση μου είναι τόσο αφύσικη και άκομψη όσο αφύσικο και άκομψο είναι το θεώρημα του Rolle, διότι τίποτε άλλο δεν χρησιμοποιεί.
Ο λόγος που είπα αφύσικη και άκομψη την λύση είναι γιατί χρησιμοποιεί σχετικά βαρειά εργαλεία για την αξία της άσκησης (δύο φορές Rolle σε ειδικά ορισμένη συνάρτηση). Το μόνο που απαιτείται για την λύση είναι να διαπιστώσει κανείς ότι η κλίση της εφαπτομένης της καμπύλης
 είναι μικρότερη του
είναι μικρότερη του  (εκτός από τα άκρα) ενώ για να διέρχεται από το εν λόγω σημείο χρειάζεται κλίση μεγαλύτερη ή ίση του
(εκτός από τα άκρα) ενώ για να διέρχεται από το εν λόγω σημείο χρειάζεται κλίση μεγαλύτερη ή ίση του  .
.Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Μια ακόμη ιδέα, ισοδύναμη με κάποιες που έχουν παρουσιαστεί, είναι η εξής:Mihalis_Lambrou έγραψε:.....
Για να δείξουμε ότι δεν υπάρχουν άλλες εφαπτόμενες που διέρχονται από τοπέρα από αυτές στα
, έστω
. Η εφαπτομένη στο
έχει κλίση
. Επίσης θα έπρεπε να έχει κλίση
, που αντιβαίνει στην
. Όμοια έχουμε άτοπο για τα υπόλοιπα
ή, εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξονα
.
Σχολιάζω/προβλέπω ότι το ερώτημα Γ1 θα έχει σχεδόν καθολική αποτυχία στα γραπτά των υποψηφίων. Ίδωμεν.
Όπως παραπάνω, έστω
 . Η
. Η  έχει κλίση
έχει κλίση  , ενώ η εφαπτομένη στο
, ενώ η εφαπτομένη στο 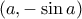 έχει κλίση
έχει κλίση 
Συνεπώς, οι δύο ευθείες τέμνονται, με το σημείο τομής τους να έχει τετμημένη η οποία είναι λύση της εξίσωσης

Γραφικά, είναι φανερό ότι η λύση αυτής βρίσκεται στο διάστημα
 Αλλιώς, για να το αποδείξουμε μπορούμε να εφαρμόσουμε Bolzano (
Αλλιώς, για να το αποδείξουμε μπορούμε να εφαρμόσουμε Bolzano (  στο
στο ![[0,a] [0,a]](/forum/ext/geomar/texintegr/latexrender/pictures/13596d6674a86fdafa24c4c414033e58.png) . Παρατηρούμε ότι είναι
. Παρατηρούμε ότι είναι  από την
από την  για
για  ή από το γεγονός ότι η
ή από το γεγονός ότι η  που σημαίνει ότι η
που σημαίνει ότι η  είναι γν. φθίνουσα στο
είναι γν. φθίνουσα στο ![[0,a] [0,a]](/forum/ext/geomar/texintegr/latexrender/pictures/13596d6674a86fdafa24c4c414033e58.png) και λόγω συνέχειας έχει μοναδική ρίζα εκεί.
και λόγω συνέχειας έχει μοναδική ρίζα εκεί.Αφού δύο μη παράλληλες ευθείες τέμνονται σε ακριβώς ένα σημείο, η παραπάνω εφαπτομένη δε διέρχεται από το

Για την εφαπτομένη στο
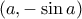 για
για  εργαζόμαστε ομοίως.
εργαζόμαστε ομοίως.Φιλικά,
Αχιλλέας
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Αχιλλέα, ακριβώς.achilleas έγραψε: Γραφικά, είναι φανερό ...
Αυτό που ήθελα να αναδείξω στο προηγούμενο ποστ μου είναι ότι η φυσιολογική απόδειξη είναι αυτή που μας καθοδηγεί το σχήμα. Παρακάτω κάνω το σχήμα της δικής μου απόδειξης (= παραλλαγής άλλων που είδαμε στο φόρουμ) όπου αναδεικνύεται η αιτία του φαινομένου
Συγκεκριμένα (για ευκολία εργάζομαι με το συμμετρικό σχήμα για να μη μπλέκουμε με αρνητικούς): Η εφαπτομένη στο
 αποκλείεται να περνά από το
αποκλείεται να περνά από το  καθώς η κλίση της
καθώς η κλίση της  είναι μικρότερη της κλίσης της
είναι μικρότερη της κλίσης της  . Αν η εν λόγω εφαπτομένη διερχόταν από το
. Αν η εν λόγω εφαπτομένη διερχόταν από το  (κόκκινη διακεκομένη γραμμή) θα όφειλε να έχει κλίση μεγαλύτερη της
(κόκκινη διακεκομένη γραμμή) θα όφειλε να έχει κλίση μεγαλύτερη της  . Αυτό ήταν όλο.
. Αυτό ήταν όλο. Η γραφή της απόδειξης που παρέθεσα έχει αυτά κατά νου (γι 'αυτό την διατυπώνω με κλίσεις) αλλά είναι με σύμβολα. Τίποτα δεν ξεπερνά την γεωμετρική εποπτεία. Όπως είπα, αναδεικνύει την αιτία. Είναι φυσιολογική.
- Συνημμένα
-
- efaptomeni panellinies.png (9.07 KiB) Προβλήθηκε 2258 φορές
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Συμφωνούμε!Mihalis_Lambrou έγραψε:Αχιλλέα, ακριβώς.achilleas έγραψε: Γραφικά, είναι φανερό ...
Αυτό που ήθελα να αναδείξω στο προηγούμενο ποστ μου είναι ότι η φυσιολογική απόδειξη είναι αυτή που μας καθοδηγεί το σχήμα. Παρακάτω κάνω το σχήμα της δικής μου απόδειξης (= παραλλαγής άλλων που είδαμε στο φόρουμ) όπου αναδεικνύεται η αιτία του φαινομένου
Συγκεκριμένα (για ευκολία εργάζομαι με το συμμετρικό σχήμα για να μη μπλέκουμε με αρνητικούς): Η εφαπτομένη στοαποκλείεται να περνά από το
καθώς η κλίση της
είναι μικρότερη της κλίσης της
. Αν η εν λόγω εφαπτομένη διερχόταν από το
(κόκκινη διακεκομένη γραμμή) θα όφειλε να έχει κλίση μεγαλύτερη της
. Αυτό ήταν όλο.
Η γραφή της απόδειξης που παρέθεσα έχει αυτά κατά νου (γι 'αυτό την διατυπώνω με κλίσεις) αλλά είναι με σύμβολα. Τίποτα δεν ξεπερνά την γεωμετρική εποπτεία. Όπως είπα, αναδεικνύει την αιτία. Είναι φυσιολογική.
Πολλές αποδείξεις στον Απειροστικό επεξηγούνται πολύ καλύτερα από ένα σχήμα.
Έτσι, ακόμα και η επιλογή μιας "βοηθητικής" συνάρτησης φαίνεται λιγότερο ουρανοκατέβατη.
Φιλικά,
Αχιλλέας
-
Παντελής Μιντεκίδης
- Δημοσιεύσεις: 15
- Εγγραφή: Τετ Μάιος 29, 2013 11:40 pm
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Αγαπητέ κύριε Μιχάλη Λάμπρου,Παντελής Μιντεκίδης έγραψε:Αγαπητέ κύριε Μιχάλη Λάμπρου,Mihalis_Lambrou έγραψε:Δεν έχω δει την επίσημη λύση της Γ1, αλλά κοίταξα διάφορες εδώ και εκεί. Γράφω άλλη μία κάπως πιο απλή αλλά στο ίδιο μήκος κύματος με τρεις στο δικό μας φόρουμ (η τέταρτη, του Παντελή Μιντεκίδη, είναι διαφορετική αλλά αρκετά αφύσικη και άκομψη).
Για να δείξουμε ότι δεν υπάρχουν άλλες εφαπτόμενες που διέρχονται από τοπέρα από αυτές στα
, έστω
. Η εφαπτομένη στο
έχει κλίση
. Επίσης θα έπρεπε να έχει κλίση
, που αντιβαίνει στην
. Όμοια έχουμε άτοπο για τα υπόλοιπα
ή, εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξονα
.
Σχολιάζω/προβλέπω ότι το ερώτημα Γ1 θα έχει σχεδόν καθολική αποτυχία στα γραπτά των υποψηφίων. Ίδωμεν.
Ευχαριστώ που κάνατε τον κόπο να ασχοληθείτε με τις λύσεις μου.
1) Εφόσον η δική μου λύση πιστεύετε ότι είναι "αρκετά αφύσικη και άκομψη", δεν μπορεί παρά επίσης να πιστεύετε ότι η δική σας λύση είναι τουλάχιστον αρκετά φυσική και κομψή.
2) Επιτρέψτε μου να μήν σχολιάσω την δική σας λύση, εκτός και αν μου το ζητήσετε.
3) Η λύση μου είναι τόσο αφύσικη και άκομψη όσο αφύσικο και άκομψο είναι το θεώρημα του Rolle, διότι τίποτε άλλο δεν χρησιμοποιεί.
4) Παρακαλώ, ρίξτε μιά ματιά στις ασκήσεις του σχολικού βιβλίου που αφορούν στο θεώρημα Rolle. Οι ασκήσεις Β3(i), B3(ii) εφαρμόζουν αυτήν την μέθοδο. Αλλά παρακάτω η άσκηση Β7 είναι ακριβώς αυτό που κάνω, σχεδόν αυτολεξεί.
Θερμούς χαιρετισμούς,
Παντελής Μιντεκίδης
Επειδή βλέπω ότι συνεχίζεται να ασχολείστε με ειρωνική διάθεση μαζί μου, με αναγκάζεται να σας πληροφορήσω ότι η λύση σας: "Όμοια έχουμε άτοπο για τα υπόλοιπα α" είναι ΛΑΘΟΣ !!! Αν πιστεύετε ότι είναι σωστή, δημοσιεύστε την όλη, δηλαδή και για α στο 2ο τεταρτημόριο, για να δούμε πόσο όμοια είναι με την περίπτωση του 1ου τεταρτημορίου και κυρίως πόσο φυσική και κομψή.
Θερμούς χαιρετισμούς,
Παντελής Μιντεκίδης
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Οι ανάλογες συνθήκες για το δεύτερο τεταρτημόριο είναι  και
και 
Μην αρπάζεσαι και μην παίρνεις προσωπικά μία κριτική. Αν είναι αβάσιμη, όλα εντάξει. Αν είναι βάσιμη, μόλις έμαθες κάτι.
 και
και 
Μην αρπάζεσαι και μην παίρνεις προσωπικά μία κριτική. Αν είναι αβάσιμη, όλα εντάξει. Αν είναι βάσιμη, μόλις έμαθες κάτι.
Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Καμία ειρωνική διάθεση. Αν θέλεις το πιστεύεις. Η ιστορία μου στο φόρουμ είναι αρκετό τεκμήριο και δεν χρειάζεται να το αιτιολογήσω.Παντελής Μιντεκίδης έγραψε: Επειδή βλέπω ότι συνεχίζεται να ασχολείστε με ειρωνική διάθεση μαζί μου,
Το "όμοια" πάει στην μέθοδο: Κλίση της εφαπτομένης, και όχι στις επιμέρους πράξεις. Άλλωστε αυτό είναι εμφανές με την φράση μου "ή εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξοναΠαντελής Μιντεκίδης έγραψε:
με αναγκάζεται να σας πληροφορήσω ότι η λύση σας: "Όμοια έχουμε άτοπο για τα υπόλοιπα α" είναι ΛΑΘΟΣ !!!
 " (μόνο που έχω αυτονόητο τυπογραφικό σφάλμα, και το σωστό είναι
" (μόνο που έχω αυτονόητο τυπογραφικό σφάλμα, και το σωστό είναι 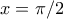 )
)Η "μονολεκτική" συμπλήρωση του συλλογισμού από τον Δημήτρη Σκουτέρη αμέσως από πάνω, τα λέει όλα. Είναι ακριβώς αυτό που έχω κατά νου.
Ακόμη καλύτερα, δώσε προσοχή στην τελευταία πρόταση του Δημήτρη Σκουτέρη. Εκεί και αν τα λέει όλα.
-
Παντελής Μιντεκίδης
- Δημοσιεύσεις: 15
- Εγγραφή: Τετ Μάιος 29, 2013 11:40 pm
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Μιχάλη Λάμπρου,Mihalis_Lambrou έγραψε:Καμία ειρωνική διάθεση. Αν θέλεις το πιστεύεις. Η ιστορία μου στο φόρουμ είναι αρκετό τεκμήριο και δεν χρειάζεται να το αιτιολογήσω.Παντελής Μιντεκίδης έγραψε: Επειδή βλέπω ότι συνεχίζεται να ασχολείστε με ειρωνική διάθεση μαζί μου,
Το "όμοια" πάει στην μέθοδο: Κλίση της εφαπτομένης, και όχι στις επιμέρους πράξεις. Άλλωστε αυτό είναι εμφανές με την φράση μου "ή εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξοναΠαντελής Μιντεκίδης έγραψε:
με αναγκάζεται να σας πληροφορήσω ότι η λύση σας: "Όμοια έχουμε άτοπο για τα υπόλοιπα α" είναι ΛΑΘΟΣ !!!" (μόνο που έχω αυτονόητο τυπογραφικό σφάλμα, και το σωστό είναι
)
Η "μονολεκτική" συμπλήρωση του συλλογισμού από τον Δημήτρη Σκουτέρη αμέσως από πάνω, τα λέει όλα. Είναι ακριβώς αυτό που έχω κατά νου.
Ακόμη καλύτερα, δώσε προσοχή στην τελευταία πρόταση του Δημήτρη Σκουτέρη. Εκεί και αν τα λέει όλα.
Ακόμη δεν είδα την απόδειξη! Αυτό που παρουσιάζει ο υποστηρικτής σας είναι εντελώς ατελές! Δέν θα μας αποδείξετε ότι: sinα+α<π ;; Για να δούμε την φυσικότητα και την κομψότητα!
Παντελής Μιντεκίδης
ΥΓ Ουδείς αρνείται την τεράστια συνεισφορά σας καθώς και των υπολοίπων συνεργατών σας στο mathematica.gr, αλλά είναι άλλο θέμα. Μια τόση δα λύση, φυσική και κομψή, σε πόσες δόσεις τέλος πάντων θα μας την παρουσιάσετε!
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Νομίζω η απόδειξη είναι αρκετά απλή και γεωμετρική έστω ορθογώνιο τρίγωνοΠαντελής Μιντεκίδης έγραψε:Μιχάλη Λάμπρου,Mihalis_Lambrou έγραψε:Καμία ειρωνική διάθεση. Αν θέλεις το πιστεύεις. Η ιστορία μου στο φόρουμ είναι αρκετό τεκμήριο και δεν χρειάζεται να το αιτιολογήσω.Παντελής Μιντεκίδης έγραψε: Επειδή βλέπω ότι συνεχίζεται να ασχολείστε με ειρωνική διάθεση μαζί μου,
Το "όμοια" πάει στην μέθοδο: Κλίση της εφαπτομένης, και όχι στις επιμέρους πράξεις. Άλλωστε αυτό είναι εμφανές με την φράση μου "ή εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξοναΠαντελής Μιντεκίδης έγραψε:
με αναγκάζεται να σας πληροφορήσω ότι η λύση σας: "Όμοια έχουμε άτοπο για τα υπόλοιπα α" είναι ΛΑΘΟΣ !!!" (μόνο που έχω αυτονόητο τυπογραφικό σφάλμα, και το σωστό είναι
)
Η "μονολεκτική" συμπλήρωση του συλλογισμού από τον Δημήτρη Σκουτέρη αμέσως από πάνω, τα λέει όλα. Είναι ακριβώς αυτό που έχω κατά νου.
Ακόμη καλύτερα, δώσε προσοχή στην τελευταία πρόταση του Δημήτρη Σκουτέρη. Εκεί και αν τα λέει όλα.
Ακόμη δεν είδα την απόδειξη! Αυτό που παρουσιάζει ο υποστηρικτής σας είναι εντελώς ατελές! Δέν θα μας αποδείξετε ότι: sinα+α<π ;; Για να δούμε την φυσικότητα και την κομψότητα!
Παντελής Μιντεκίδης
ΥΓ Ουδείς αρνείται την τεράστια συνεισφορά σας καθώς και των υπολοίπων συνεργατών σας στο mathematica.gr, αλλά είναι άλλο θέμα. Μια τόση δα λύση, φυσική και κομψή, σε πόσες δόσεις τέλος πάντων θα μας την παρουσιάσετε!
 με
με  ορθή και σημείο
ορθή και σημείο  στο εσωτερικό του. Από το
στο εσωτερικό του. Από το  φέρουμε ευθεία
φέρουμε ευθεία  η οποία σχηματίζει γωνία
η οποία σχηματίζει γωνία
με την
 με
με τότε προφανώς η
τότε προφανώς η  δεν διέρχεται από το
δεν διέρχεται από το  αφού βρίσκεται στο κίτρινο χώρο
αφού βρίσκεται στο κίτρινο χώρο- Συνημμένα
-
- g11.png (23.64 KiB) Προβλήθηκε 2046 φορές
-
Παντελής Μιντεκίδης
- Δημοσιεύσεις: 15
- Εγγραφή: Τετ Μάιος 29, 2013 11:40 pm
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Μιχάλη Λάμπρου και Δημήτρη Σκουτέρη,mikemoke έγραψε:Νομίζω η απόδειξη είναι αρκετά απλή και γεωμετρική έστω ορθογώνιο τρίγωνοΠαντελής Μιντεκίδης έγραψε:Μιχάλη Λάμπρου,Mihalis_Lambrou έγραψε:Καμία ειρωνική διάθεση. Αν θέλεις το πιστεύεις. Η ιστορία μου στο φόρουμ είναι αρκετό τεκμήριο και δεν χρειάζεται να το αιτιολογήσω.Παντελής Μιντεκίδης έγραψε: Επειδή βλέπω ότι συνεχίζεται να ασχολείστε με ειρωνική διάθεση μαζί μου,
Το "όμοια" πάει στην μέθοδο: Κλίση της εφαπτομένης, και όχι στις επιμέρους πράξεις. Άλλωστε αυτό είναι εμφανές με την φράση μου "ή εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξοναΠαντελής Μιντεκίδης έγραψε:
με αναγκάζεται να σας πληροφορήσω ότι η λύση σας: "Όμοια έχουμε άτοπο για τα υπόλοιπα α" είναι ΛΑΘΟΣ !!!" (μόνο που έχω αυτονόητο τυπογραφικό σφάλμα, και το σωστό είναι
)
Η "μονολεκτική" συμπλήρωση του συλλογισμού από τον Δημήτρη Σκουτέρη αμέσως από πάνω, τα λέει όλα. Είναι ακριβώς αυτό που έχω κατά νου.
Ακόμη καλύτερα, δώσε προσοχή στην τελευταία πρόταση του Δημήτρη Σκουτέρη. Εκεί και αν τα λέει όλα.
Ακόμη δεν είδα την απόδειξη! Αυτό που παρουσιάζει ο υποστηρικτής σας είναι εντελώς ατελές! Δέν θα μας αποδείξετε ότι: sinα+α<π ;; Για να δούμε την φυσικότητα και την κομψότητα!
Παντελής Μιντεκίδης
ΥΓ Ουδείς αρνείται την τεράστια συνεισφορά σας καθώς και των υπολοίπων συνεργατών σας στο mathematica.gr, αλλά είναι άλλο θέμα. Μια τόση δα λύση, φυσική και κομψή, σε πόσες δόσεις τέλος πάντων θα μας την παρουσιάσετε!με
ορθή και σημείο
στο εσωτερικό του. Από το
φέρουμε ευθεία
η οποία σχηματίζει γωνία
με τηνμε
τότε προφανώς η
δεν διέρχεται από το
αφού βρίσκεται στο κίτρινο χώρο
Αφήστε τους "γεωμετρικούς" παρελκισμούς! Για τελευταία φορά σας παρακαλώ! Δώστε το έσχατο μέρος της απόδειξης, δηλαδή: sinα+α<π, ώστε να ολοκληρώσετε την φυσική και κομψή σας απόδειξη!!!
Παντελής Μιντεκίδης
Re: Μαθηματικά προσανατολισμού 2017 (Θέματα & Λύσεις)
Η γεωμετρία δεν ήταν δική μου, αλλά εν πάση περιπτώσει. Επειδή δεν φαίνεσαι να προβάλλεις ένσταση στηνΠαντελής Μιντεκίδης έγραψε: Μιχάλη Λάμπρου και Δημήτρη Σκουτέρη,
Αφήστε τους "γεωμετρικούς" παρελκισμούς! Για τελευταία φορά σας παρακαλώ! Δώστε το έσχατο μέρος της απόδειξης, δηλαδή: sinα+α<π, ώστε να ολοκληρώσετε την φυσική και κομψή σας απόδειξη!!!
Παντελής Μιντεκίδης
 , (που χρησιμοποιείται στο πρώτο τεταρτημόριο), υποθέτω ότι τη θεωρείς δεδομένη.
, (που χρησιμοποιείται στο πρώτο τεταρτημόριο), υποθέτω ότι τη θεωρείς δεδομένη.Λοιπόν (για δεύτερη φορά, δεν θα υπάρξει τρίτη)
 .
.Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες


![\displaystyle{[1,e]} \displaystyle{[1,e]}](/forum/ext/geomar/texintegr/latexrender/pictures/e45e9c214f89168d99bc56eea3406327.png)

