ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 2015
- Christos75
- Δημοσιεύσεις: 422
- Εγγραφή: Δευ Φεβ 02, 2009 9:41 pm
- Τοποθεσία: Athens
- Επικοινωνία:
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 2015
Σήμερα είναι η εξέταση των Μαθηματικών Γενικής Παιδείας στη σειρά των επαναληπτικών εξετάσεων.
Εδώ θα αναρτήσουμε και θα συζητήσουμε τα θέματα μόλις ανακοινωθούν επίσημα από το υπουργείο παιδείας.
Καλή τύχη στα παιδιά!
Εδώ θα αναρτήσουμε και θα συζητήσουμε τα θέματα μόλις ανακοινωθούν επίσημα από το υπουργείο παιδείας.
Καλή τύχη στα παιδιά!
Χρήστος Λοΐζος
- Γιώργος Απόκης
- Διευθύνον Μέλος
- Δημοσιεύσεις: 5092
- Εγγραφή: Δευ Μάιος 16, 2011 7:56 pm
- Τοποθεσία: Πάτρα
- Επικοινωνία:
Re: ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 2015
ΘΕΜΑ Β
Β1. H συνάρτηση είναι παραγωγίσιμη στο με
με  . Αφού η γραφική παράσταση εφάπτεται του
. Αφού η γραφική παράσταση εφάπτεται του 
στο θα ισχύουν :
θα ισχύουν : 
B2. Έχουμε



 H συνάρτηση είναι γνησίως αύξουσα σε καθένα από τα διαστήματα
H συνάρτηση είναι γνησίως αύξουσα σε καθένα από τα διαστήματα ![\displaystyle{(-\infty,-2],~[0,+\infty)} \displaystyle{(-\infty,-2],~[0,+\infty)}](/forum/ext/geomar/texintegr/latexrender/pictures/de0378769810dcd0a12f86c5ee76cb17.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![\displaystyle{[-2,0]} \displaystyle{[-2,0]}](/forum/ext/geomar/texintegr/latexrender/pictures/1f418e328ed79e3000ad4fedd261a1d0.png)
 Η συνάρτηση παρουσιάζει τοπικό μέγιστο το
Η συνάρτηση παρουσιάζει τοπικό μέγιστο το  και τοπικό ελάχιστο το
και τοπικό ελάχιστο το  .
.
B3. O συντελεστής διεύθυνσης της εφαπτομένης στο τυχαίο σημείο M δίνεται από την
δίνεται από την
 η οποία είναι παραγωγίσιμη με
η οποία είναι παραγωγίσιμη με  .
.



Eπομένως, ο συντελεστής διεύθυνσης γίνεται ελάχιστος στο
B4. Έχουμε

Β1. H συνάρτηση είναι παραγωγίσιμη στο
 με
με  . Αφού η γραφική παράσταση εφάπτεται του
. Αφού η γραφική παράσταση εφάπτεται του 
στο
 θα ισχύουν :
θα ισχύουν : 
B2. Έχουμε




 H συνάρτηση είναι γνησίως αύξουσα σε καθένα από τα διαστήματα
H συνάρτηση είναι γνησίως αύξουσα σε καθένα από τα διαστήματα ![\displaystyle{(-\infty,-2],~[0,+\infty)} \displaystyle{(-\infty,-2],~[0,+\infty)}](/forum/ext/geomar/texintegr/latexrender/pictures/de0378769810dcd0a12f86c5ee76cb17.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![\displaystyle{[-2,0]} \displaystyle{[-2,0]}](/forum/ext/geomar/texintegr/latexrender/pictures/1f418e328ed79e3000ad4fedd261a1d0.png)
 Η συνάρτηση παρουσιάζει τοπικό μέγιστο το
Η συνάρτηση παρουσιάζει τοπικό μέγιστο το  και τοπικό ελάχιστο το
και τοπικό ελάχιστο το  .
.B3. O συντελεστής διεύθυνσης της εφαπτομένης στο τυχαίο σημείο M
 δίνεται από την
δίνεται από την η οποία είναι παραγωγίσιμη με
η οποία είναι παραγωγίσιμη με  .
.


Eπομένως, ο συντελεστής διεύθυνσης γίνεται ελάχιστος στο

B4. Έχουμε


Γιώργος
- Christos75
- Δημοσιεύσεις: 422
- Εγγραφή: Δευ Φεβ 02, 2009 9:41 pm
- Τοποθεσία: Athens
- Επικοινωνία:
Re: ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 2015
ΘΕΜΑ Β
Β1. Πρέπει να ισχύoυν :
1)
2)
Από όπου έχουμε με την επίλυση του συστήματος ότι
Β2. Αναζητούμε την μονοτονία της δοθείσας συνάρτησης και έχουμε:
 από όπου κάνοντας πίνακα τιμών και επικαλούμενοι το πρόσημο τριωνύμου προκύπτουν τα εξής διαστήματα μονοτονίας της f. Η συνάρτηση f είναι: γνησίως αύξουσα στο διάστημα
από όπου κάνοντας πίνακα τιμών και επικαλούμενοι το πρόσημο τριωνύμου προκύπτουν τα εξής διαστήματα μονοτονίας της f. Η συνάρτηση f είναι: γνησίως αύξουσα στο διάστημα ![(-\infty ,-2] (-\infty ,-2]](/forum/ext/geomar/texintegr/latexrender/pictures/9816f31e63115b479dd8ff4237138094.png) γνησίως φθίνουσα στο διάστημα
γνησίως φθίνουσα στο διάστημα ![[-2,0] [-2,0]](/forum/ext/geomar/texintegr/latexrender/pictures/5743178200081e6d6488c773516b1c6f.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  . Συνεπώς η συνάρτηση έχει ένα ελάχιστο και ένα μέγιστο, μέγιστο στο σημείο
. Συνεπώς η συνάρτηση έχει ένα ελάχιστο και ένα μέγιστο, μέγιστο στο σημείο  και ελάχιστο στο
και ελάχιστο στο 
B3. Το ζητούμενο σημείο το βρίσκουμε ως εξής: Θεωρώ συνάρτηση την οποία και παραγωγίζω για να βρω τη μονοτονία και το ακρότατό της.
την οποία και παραγωγίζω για να βρω τη μονοτονία και το ακρότατό της.
Πράγματι μετά από την παραγώγιση έχω: Οπότε
Οπότε  και
και  Άρα στο σημείο με τετμημένη
Άρα στο σημείο με τετμημένη  η
η  ελαχιστοποιείται. Συνεπώς το ζητούμενο σημείο του γραφήματος της f είναι το
ελαχιστοποιείται. Συνεπώς το ζητούμενο σημείο του γραφήματος της f είναι το 
Β4. Εύκολα παρατηρούμε ότι εάν θέσουμε όπου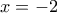 θα λάβουμε απροσδιοριστία
θα λάβουμε απροσδιοριστία  Παίρνοντας τη συζυγή παράσταση του παρονομαστή θα έχουμε:
Παίρνοντας τη συζυγή παράσταση του παρονομαστή θα έχουμε: 
Με πρόλαβε ο αγαπητός Γιώργος...λέω να το αφήσω για τον κόπο. Οι συντονιστές θα κρίνουν αν πρέπει να σβηστεί τελικά ή όχι...
Β1. Πρέπει να ισχύoυν :
1)

2)

Από όπου έχουμε με την επίλυση του συστήματος ότι

Β2. Αναζητούμε την μονοτονία της δοθείσας συνάρτησης και έχουμε:
 από όπου κάνοντας πίνακα τιμών και επικαλούμενοι το πρόσημο τριωνύμου προκύπτουν τα εξής διαστήματα μονοτονίας της f. Η συνάρτηση f είναι: γνησίως αύξουσα στο διάστημα
από όπου κάνοντας πίνακα τιμών και επικαλούμενοι το πρόσημο τριωνύμου προκύπτουν τα εξής διαστήματα μονοτονίας της f. Η συνάρτηση f είναι: γνησίως αύξουσα στο διάστημα ![(-\infty ,-2] (-\infty ,-2]](/forum/ext/geomar/texintegr/latexrender/pictures/9816f31e63115b479dd8ff4237138094.png) γνησίως φθίνουσα στο διάστημα
γνησίως φθίνουσα στο διάστημα ![[-2,0] [-2,0]](/forum/ext/geomar/texintegr/latexrender/pictures/5743178200081e6d6488c773516b1c6f.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  . Συνεπώς η συνάρτηση έχει ένα ελάχιστο και ένα μέγιστο, μέγιστο στο σημείο
. Συνεπώς η συνάρτηση έχει ένα ελάχιστο και ένα μέγιστο, μέγιστο στο σημείο  και ελάχιστο στο
και ελάχιστο στο 
B3. Το ζητούμενο σημείο το βρίσκουμε ως εξής: Θεωρώ συνάρτηση
 την οποία και παραγωγίζω για να βρω τη μονοτονία και το ακρότατό της.
την οποία και παραγωγίζω για να βρω τη μονοτονία και το ακρότατό της.Πράγματι μετά από την παραγώγιση έχω:
 Οπότε
Οπότε  και
και  Άρα στο σημείο με τετμημένη
Άρα στο σημείο με τετμημένη  η
η  ελαχιστοποιείται. Συνεπώς το ζητούμενο σημείο του γραφήματος της f είναι το
ελαχιστοποιείται. Συνεπώς το ζητούμενο σημείο του γραφήματος της f είναι το 
Β4. Εύκολα παρατηρούμε ότι εάν θέσουμε όπου
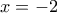 θα λάβουμε απροσδιοριστία
θα λάβουμε απροσδιοριστία  Παίρνοντας τη συζυγή παράσταση του παρονομαστή θα έχουμε:
Παίρνοντας τη συζυγή παράσταση του παρονομαστή θα έχουμε: 
Με πρόλαβε ο αγαπητός Γιώργος...λέω να το αφήσω για τον κόπο. Οι συντονιστές θα κρίνουν αν πρέπει να σβηστεί τελικά ή όχι...
Χρήστος Λοΐζος
- Christos75
- Δημοσιεύσεις: 422
- Εγγραφή: Δευ Φεβ 02, 2009 9:41 pm
- Τοποθεσία: Athens
- Επικοινωνία:
Re: ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 2015
ΘΕΜΑ Α
Α1. Θεωρία σχολικού βιβλίου σελίδα 150.
Α2. Θεωρία σχολικού βιβλίου σελίδα 16.
Α3. Θεωρία σχολικού βιβλίου σελίδα 96.
Α4.
α) Λάθος
β) Σωστό
γ) Σωστό
δ) Λάθος
ε) Λάθος
Α1. Θεωρία σχολικού βιβλίου σελίδα 150.
Α2. Θεωρία σχολικού βιβλίου σελίδα 16.
Α3. Θεωρία σχολικού βιβλίου σελίδα 96.
Α4.
α) Λάθος
β) Σωστό
γ) Σωστό
δ) Λάθος
ε) Λάθος
Χρήστος Λοΐζος
-
Θεοδωρος Παγωνης
- Δημοσιεύσεις: 311
- Εγγραφή: Τετ Οκτ 26, 2011 2:10 pm
- Τοποθεσία: Αγρίνιο
Re: ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 2015
Έστω  το πλάτος των κλάσεων. Επειδή η μικρότερη διάρκεια είναι 0 και η κεντρική τιμή της 5ης κλάσης είναι 18
το πλάτος των κλάσεων. Επειδή η μικρότερη διάρκεια είναι 0 και η κεντρική τιμή της 5ης κλάσης είναι 18
θα έχουμε

Γ2. Η γωνία του κυκλικού τομέα που αντιστοιχεί στην 5η κλάση είναι 36ο , επομένως θα έχουμε :

Οπότε

Είναι

Οπότε
 ,
,  ,
,  ,
, 
Επομένως θα έχουμε :




Επίσης

Όμως :

Άρα :




Γ3. Το ποσοστό των συνδρομητών του δείγματος που έχουν χρεωθεί τουλάχιστον 3 ώρες και λιγότερο από 10 ώρες ομιλίας είναι:
Γ4. Έχουμε






Υ.Γ. Δεν μπόρεσα να κατασκευάσω (σε latex) τους πίνακες.
 το πλάτος των κλάσεων. Επειδή η μικρότερη διάρκεια είναι 0 και η κεντρική τιμή της 5ης κλάσης είναι 18
το πλάτος των κλάσεων. Επειδή η μικρότερη διάρκεια είναι 0 και η κεντρική τιμή της 5ης κλάσης είναι 18 θα έχουμε

Γ2. Η γωνία του κυκλικού τομέα που αντιστοιχεί στην 5η κλάση είναι 36ο , επομένως θα έχουμε :

Οπότε

Είναι

Οπότε
 ,
,  ,
,  ,
, 
Επομένως θα έχουμε :




Επίσης

Όμως :

Άρα :




Γ3. Το ποσοστό των συνδρομητών του δείγματος που έχουν χρεωθεί τουλάχιστον 3 ώρες και λιγότερο από 10 ώρες ομιλίας είναι:

Γ4. Έχουμε






Υ.Γ. Δεν μπόρεσα να κατασκευάσω (σε latex) τους πίνακες.
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 2015
Ξεκινώ το Θέμα Δ.
Δ1. Τα ορθογώνια τρίγωνα είναι ίσα μεταξύ τους, γιατί έχουν κάθετες πλευρές ίσες με
είναι ίσα μεταξύ τους, γιατί έχουν κάθετες πλευρές ίσες με  και
και  αντίστοιχα κι έχουν εμβαδόν
αντίστοιχα κι έχουν εμβαδόν  .
.
(ΣΧΟΛΙΟ: Προτιμήσαμε τον υπολογισμό του εμβαδού ως διαφορά άλλων, γιατί αν υπολογίζαμε τη πλευρά του , από Πυθαγόρειο θεώρημα, θα έπρεπε να αποδείξουμε (εύκολα) και ότι είναι ορθές οι γωνίες του)
, από Πυθαγόρειο θεώρημα, θα έπρεπε να αποδείξουμε (εύκολα) και ότι είναι ορθές οι γωνίες του)
Οπότε
Η συνάρτηση είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  .
.
Δ2. Είναι για
για  ,
,  και
και  για
για  , οπότε η συνάρτηση έχει ελάχιστο για
, οπότε η συνάρτηση έχει ελάχιστο για  .
.
Δ3.
α) Είναι


β)

 , οπότε είναι ομογενές το δείγμα.
, οπότε είναι ομογενές το δείγμα.
γ)
Αφού είναι , και τα
, και τα  είναι θετικά και ανά δύο διαφορετικά μεταξύ τους, τότε
είναι θετικά και ανά δύο διαφορετικά μεταξύ τους, τότε  και
και 
Οπότε , άρα
, άρα 
Είναι άρα
άρα 
Δεν πραγματοποιείται κανένα από τα και
και  όταν
όταν  , οπότε
, οπότε 
Δ1. Τα ορθογώνια τρίγωνα
 είναι ίσα μεταξύ τους, γιατί έχουν κάθετες πλευρές ίσες με
είναι ίσα μεταξύ τους, γιατί έχουν κάθετες πλευρές ίσες με  και
και  αντίστοιχα κι έχουν εμβαδόν
αντίστοιχα κι έχουν εμβαδόν  .
.(ΣΧΟΛΙΟ: Προτιμήσαμε τον υπολογισμό του εμβαδού ως διαφορά άλλων, γιατί αν υπολογίζαμε τη πλευρά του
 , από Πυθαγόρειο θεώρημα, θα έπρεπε να αποδείξουμε (εύκολα) και ότι είναι ορθές οι γωνίες του)
, από Πυθαγόρειο θεώρημα, θα έπρεπε να αποδείξουμε (εύκολα) και ότι είναι ορθές οι γωνίες του)Οπότε

Η συνάρτηση
 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  .
.Δ2. Είναι
 για
για  ,
,  και
και  για
για  , οπότε η συνάρτηση έχει ελάχιστο για
, οπότε η συνάρτηση έχει ελάχιστο για  .
.Δ3.
α) Είναι


β)


 , οπότε είναι ομογενές το δείγμα.
, οπότε είναι ομογενές το δείγμα.γ)
Αφού είναι
 , και τα
, και τα  είναι θετικά και ανά δύο διαφορετικά μεταξύ τους, τότε
είναι θετικά και ανά δύο διαφορετικά μεταξύ τους, τότε  και
και 
Οπότε
 , άρα
, άρα 
Είναι
 άρα
άρα 
Δεν πραγματοποιείται κανένα από τα
 και
και  όταν
όταν  , οπότε
, οπότε 
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες
