Μαθηματικά κατεύθυνσης 2015
-
Επιτροπή Θεμάτων 15
- Δημοσιεύσεις: 8
- Εγγραφή: Τετ Μάιος 20, 2015 9:51 am
Μαθηματικά κατεύθυνσης 2015
Αγαπητές/τοί φίλες/οι
Στο θέμα αυτό θα συζητήσουμε αποκλειστικά τα θέματα των Μαθηματικών κατεύθυνσης 2015 αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου.
Στο θέμα αυτό θα συζητήσουμε αποκλειστικά τα θέματα των Μαθηματικών κατεύθυνσης 2015 αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου.
Επιτροπή Θεμάτων 2015
-
Επιτροπή Θεμάτων 15
- Δημοσιεύσεις: 8
- Εγγραφή: Τετ Μάιος 20, 2015 9:51 am
Re: Μαθηματικά κατεύθυνσης 2015
Τα θέματα που μόλις δημοσιεύθηκαν στη σελίδα του Υπουργείου.
Επιτροπή Θεμάτων 2015
Re: Μαθηματικά κατεύθυνσης 2015
Για το Α θέμα:
Α1) Απόδειξη σελίδα 194 σχολικού βιβλίου
Α2) Ορισμός σελίδα 188 σχολικού βιβλίου
Α3) Ορισμός σελίδα 259 σχολικού βιβλίου
Α4) α) Λ (σελίδα 144 σχολικού βιβλίου)
β) Σ (σελίδα 89 σχολικού βιβλίου)
γ) Λ (σελίδα 225 σχολικού βιβλίου)
δ) Σ (σελίδα 332 σχολικού βιβλίου)
ε) Σ (σελίδα 178 σχολικού βιβλίου)
Α1) Απόδειξη σελίδα 194 σχολικού βιβλίου
Α2) Ορισμός σελίδα 188 σχολικού βιβλίου
Α3) Ορισμός σελίδα 259 σχολικού βιβλίου
Α4) α) Λ (σελίδα 144 σχολικού βιβλίου)
β) Σ (σελίδα 89 σχολικού βιβλίου)
γ) Λ (σελίδα 225 σχολικού βιβλίου)
δ) Σ (σελίδα 332 σχολικού βιβλίου)
ε) Σ (σελίδα 178 σχολικού βιβλίου)
Re: Μαθηματικά κατεύθυνσης 2015
Θέμα Β.
Β.1 Έστω .Τότε η δοσμένη σχέση γράφεται
.Τότε η δοσμένη σχέση γράφεται  .
.
Ισοδύναμα άρα οι εικόνες των
άρα οι εικόνες των 
ανήκουν στον κύκλο κέντρου και ακτίνας
και ακτίνας  .
.
B.2 α) Ισχύει κατ' αρχάς για κάθε
για κάθε  του παραπάνω ερωτήματος.
του παραπάνω ερωτήματος.
Άρα και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε.
Β.3 Αρκεί .
.
Όμως και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε.
Β.4 .
.
Άρα οι εικόνες τους είναι αντιδιαμετρικά σημεία του κύκλου (ή αλλιώς συμμετρικές ως προς την αρχή των αξόνων).
Έχουμε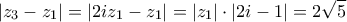 .
.
Επίσης αφού έχουμε
έχουμε  .
.
Επομένως και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε.
Β.1 Έστω
 .Τότε η δοσμένη σχέση γράφεται
.Τότε η δοσμένη σχέση γράφεται  .
.Ισοδύναμα
 άρα οι εικόνες των
άρα οι εικόνες των 
ανήκουν στον κύκλο κέντρου
 και ακτίνας
και ακτίνας  .
.B.2 α) Ισχύει κατ' αρχάς
 για κάθε
για κάθε  του παραπάνω ερωτήματος.
του παραπάνω ερωτήματος.Άρα
 και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε.Β.3 Αρκεί
 .
.Όμως
 και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε.Β.4
 .
.Άρα οι εικόνες τους είναι αντιδιαμετρικά σημεία του κύκλου (ή αλλιώς συμμετρικές ως προς την αρχή των αξόνων).
Έχουμε
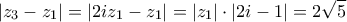 .
.Επίσης αφού
 έχουμε
έχουμε  .
.Επομένως
 και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε.Γιώργος Γαβριλόπουλος
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2015
Για το Δ4
Ορίζουμε τη συνάρτηση η οποία είναι συνεχής στο
η οποία είναι συνεχής στο ![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png) με
με
 και
και

Όμως έχουμε δείξει στο Δ2 ότι , για κάθε
, για κάθε  ( είναι κοίλη και η
( είναι κοίλη και η  είναι η εφαπτομένη της
είναι η εφαπτομένη της  στο
στο  ) με ισότητα μόνο στο
) με ισότητα μόνο στο  .
.
Άρα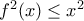 οπότε
οπότε  . Άρα
. Άρα 
Όμοια από την (θέτοντας όπου
(θέτοντας όπου  το
το  ) παίρνουμε
) παίρνουμε  και έτσι
και έτσι  . Άρα
. Άρα 
Συνεπώς κι έτσι από το θεώρημα Bolzano υπάρχει
κι έτσι από το θεώρημα Bolzano υπάρχει  ώστε
ώστε  δηλαδή ισοδύναμα (αφού
δηλαδή ισοδύναμα (αφού  ) η εξίσωση
) η εξίσωση
 έχει μία τουλάχιστον λύση στο
έχει μία τουλάχιστον λύση στο  .
.
Αλέξανδρος
Ορίζουμε τη συνάρτηση
 η οποία είναι συνεχής στο
η οποία είναι συνεχής στο ![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png) με
με και
και 
Όμως έχουμε δείξει στο Δ2 ότι
 , για κάθε
, για κάθε  ( είναι κοίλη και η
( είναι κοίλη και η  είναι η εφαπτομένη της
είναι η εφαπτομένη της  στο
στο  ) με ισότητα μόνο στο
) με ισότητα μόνο στο  .
.Άρα
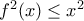 οπότε
οπότε  . Άρα
. Άρα 
Όμοια από την
 (θέτοντας όπου
(θέτοντας όπου  το
το  ) παίρνουμε
) παίρνουμε  και έτσι
και έτσι  . Άρα
. Άρα 
Συνεπώς
 κι έτσι από το θεώρημα Bolzano υπάρχει
κι έτσι από το θεώρημα Bolzano υπάρχει  ώστε
ώστε  δηλαδή ισοδύναμα (αφού
δηλαδή ισοδύναμα (αφού  ) η εξίσωση
) η εξίσωση  έχει μία τουλάχιστον λύση στο
έχει μία τουλάχιστον λύση στο  .
.Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Μαθηματικά κατεύθυνσης 2015
Και του χρόνου !
Εύχομαι καλά αποτελέσματα στους μαθητές που είναι μέλη μας αλλά και σε όλους τους μαθητές !
Εμείς τα λύσαμε από τις 8:30 στο σχολείο,στην επιτροπή , χαρείτε τα και σεις (θα βρείτε όμως και δυσκολίες ) .
Αν μετά τις λύσεις σας δω ότι έχω κάτι διαφορετικό, θα ξανάρθω !
Μπάμπης
Εύχομαι καλά αποτελέσματα στους μαθητές που είναι μέλη μας αλλά και σε όλους τους μαθητές !
Εμείς τα λύσαμε από τις 8:30 στο σχολείο,στην επιτροπή , χαρείτε τα και σεις (θα βρείτε όμως και δυσκολίες ) .
Αν μετά τις λύσεις σας δω ότι έχω κάτι διαφορετικό, θα ξανάρθω !
Μπάμπης
- exdx
- Επιμελητής
- Δημοσιεύσεις: 1741
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2015
Γ1.
Η συνάρτηση ορίζεται σε όλο το
ορίζεται σε όλο το  και είναι παραγωγίσιμη στο
και είναι παραγωγίσιμη στο  ως πηλίκο των παραγωγίσιμων συναρτήσεων
ως πηλίκο των παραγωγίσιμων συναρτήσεων 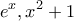 με
με 
Είναι προφανές ότι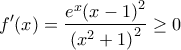 , επομένως η
, επομένως η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
Επίσης :
 ,
,
αφού : , και :
, και :

Ακόμα : Οι συναρτήσεις ,
,  είναι παραγωγίσιμες και
είναι παραγωγίσιμες και  ,
,  , και το όριο
, και το όριο  υπάρχει , όπως φαίνεται παρακάτω , επομένως ισχύουν οι προυποθέσεις εφαρμογής του κανόνα De L’ Hospital ,
υπάρχει , όπως φαίνεται παρακάτω , επομένως ισχύουν οι προυποθέσεις εφαρμογής του κανόνα De L’ Hospital ,
Άρα :
Επομένως το σύνολο τιμών είναι το
Η συνάρτηση
 ορίζεται σε όλο το
ορίζεται σε όλο το  και είναι παραγωγίσιμη στο
και είναι παραγωγίσιμη στο  ως πηλίκο των παραγωγίσιμων συναρτήσεων
ως πηλίκο των παραγωγίσιμων συναρτήσεων 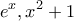 με
με 
Είναι προφανές ότι
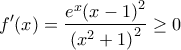 , επομένως η
, επομένως η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
Επίσης :
 ,
, αφού :
 , και :
, και :
Ακόμα : Οι συναρτήσεις
 ,
,  είναι παραγωγίσιμες και
είναι παραγωγίσιμες και  ,
,  , και το όριο
, και το όριο  υπάρχει , όπως φαίνεται παρακάτω , επομένως ισχύουν οι προυποθέσεις εφαρμογής του κανόνα De L’ Hospital ,
υπάρχει , όπως φαίνεται παρακάτω , επομένως ισχύουν οι προυποθέσεις εφαρμογής του κανόνα De L’ Hospital ,Άρα :

Επομένως το σύνολο τιμών είναι το

Kαλαθάκης Γιώργης
Re: Μαθηματικά κατεύθυνσης 2015
Θέμα Δ.
Δ.1 Η σχέση γράφεται .
.
Αφού παίρνουμε τελικά
παίρνουμε τελικά  την οποία λύνουμε σαν δευτεροβάθμια ως προς
την οποία λύνουμε σαν δευτεροβάθμια ως προς  .
.
Βρίσκουμε .Η ρίζα
.Η ρίζα  απορρίπτεται γιατί είναι πάντα αρνητική.
απορρίπτεται γιατί είναι πάντα αρνητική.
Επομένως .
.
Δ.2 α.Έχουμε .
.
Άρα .Ο παρονομαστής είναι πάντα θετικός.Ο αριθμητής αλλάζει πρόσημο μόνο στο
.Ο παρονομαστής είναι πάντα θετικός.Ο αριθμητής αλλάζει πρόσημο μόνο στο  .
.
Ισχύει για
για  και
και  για
για  .
.
Άρα η είναι κυρτή στο
είναι κυρτή στο  και κοίλη στο
και κοίλη στο  ενώ το
ενώ το  είναι το σημείο καμπής της
είναι το σημείο καμπής της  .
.
β. Μας ζητείται το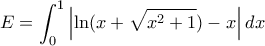 .
.
Αρχικά μελετάμε τη συνάρτηση .Αυτή είναι παραγωγίσιμη ως άθροισμα παραγωγίσιμων με
.Αυτή είναι παραγωγίσιμη ως άθροισμα παραγωγίσιμων με  .
.
Αυτό για είναι αρνητικό αφού
είναι αρνητικό αφού  ενώ για
ενώ για  μηδενίζεται.
μηδενίζεται.
Άρα η είναι γνησίως φθίνουσα.Επίσης
είναι γνησίως φθίνουσα.Επίσης 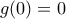 άρα
άρα 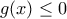 για
για  .
.
Τελικά .
.
Έχουμε![\displaystyle{\int_{0}^{1}\ln (x+\sqrt{x^2+1})dx=[x\ln (x+\sqrt{x^2+1})]_{0}^{1}-\int_{0}^{1} x\cdot \frac{1}{\sqrt{x^2+1}}dx=\ln (1+\sqrt{2})-\int_{0}^{1} \frac{2x}{2\sqrt{x^2+1}}dx} \displaystyle{\int_{0}^{1}\ln (x+\sqrt{x^2+1})dx=[x\ln (x+\sqrt{x^2+1})]_{0}^{1}-\int_{0}^{1} x\cdot \frac{1}{\sqrt{x^2+1}}dx=\ln (1+\sqrt{2})-\int_{0}^{1} \frac{2x}{2\sqrt{x^2+1}}dx}](/forum/ext/geomar/texintegr/latexrender/pictures/f37318d689093bc5a879c643f6e8366f.png)
![\displaystyle{=\ln (1+\sqrt{2})-[\sqrt{x^2+1}]_{0}^{1}=\ln(1+\sqrt{2})-(\sqrt{2}-1)} \displaystyle{=\ln (1+\sqrt{2})-[\sqrt{x^2+1}]_{0}^{1}=\ln(1+\sqrt{2})-(\sqrt{2}-1)}](/forum/ext/geomar/texintegr/latexrender/pictures/2874e6f835c7bf10a0cdeeb4ca8a321c.png) .
.
Επίσης .Τελικά
.Τελικά  .
.
Μέχρι εδώ έχω φτάσει,θα ακολουθήσουν και τα υπόλοιπα 2.
Δ.1 Η σχέση γράφεται
 .
.Αφού
 παίρνουμε τελικά
παίρνουμε τελικά  την οποία λύνουμε σαν δευτεροβάθμια ως προς
την οποία λύνουμε σαν δευτεροβάθμια ως προς  .
.Βρίσκουμε
 .Η ρίζα
.Η ρίζα  απορρίπτεται γιατί είναι πάντα αρνητική.
απορρίπτεται γιατί είναι πάντα αρνητική.Επομένως
 .
.Δ.2 α.Έχουμε
 .
.Άρα
 .Ο παρονομαστής είναι πάντα θετικός.Ο αριθμητής αλλάζει πρόσημο μόνο στο
.Ο παρονομαστής είναι πάντα θετικός.Ο αριθμητής αλλάζει πρόσημο μόνο στο  .
.Ισχύει
 για
για  και
και  για
για  .
.Άρα η
 είναι κυρτή στο
είναι κυρτή στο  και κοίλη στο
και κοίλη στο  ενώ το
ενώ το  είναι το σημείο καμπής της
είναι το σημείο καμπής της  .
.β. Μας ζητείται το
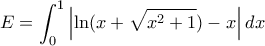 .
.Αρχικά μελετάμε τη συνάρτηση
 .Αυτή είναι παραγωγίσιμη ως άθροισμα παραγωγίσιμων με
.Αυτή είναι παραγωγίσιμη ως άθροισμα παραγωγίσιμων με  .
.Αυτό για
 είναι αρνητικό αφού
είναι αρνητικό αφού  ενώ για
ενώ για  μηδενίζεται.
μηδενίζεται.Άρα η
 είναι γνησίως φθίνουσα.Επίσης
είναι γνησίως φθίνουσα.Επίσης 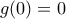 άρα
άρα 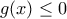 για
για  .
.Τελικά
 .
.Έχουμε
![\displaystyle{\int_{0}^{1}\ln (x+\sqrt{x^2+1})dx=[x\ln (x+\sqrt{x^2+1})]_{0}^{1}-\int_{0}^{1} x\cdot \frac{1}{\sqrt{x^2+1}}dx=\ln (1+\sqrt{2})-\int_{0}^{1} \frac{2x}{2\sqrt{x^2+1}}dx} \displaystyle{\int_{0}^{1}\ln (x+\sqrt{x^2+1})dx=[x\ln (x+\sqrt{x^2+1})]_{0}^{1}-\int_{0}^{1} x\cdot \frac{1}{\sqrt{x^2+1}}dx=\ln (1+\sqrt{2})-\int_{0}^{1} \frac{2x}{2\sqrt{x^2+1}}dx}](/forum/ext/geomar/texintegr/latexrender/pictures/f37318d689093bc5a879c643f6e8366f.png)
![\displaystyle{=\ln (1+\sqrt{2})-[\sqrt{x^2+1}]_{0}^{1}=\ln(1+\sqrt{2})-(\sqrt{2}-1)} \displaystyle{=\ln (1+\sqrt{2})-[\sqrt{x^2+1}]_{0}^{1}=\ln(1+\sqrt{2})-(\sqrt{2}-1)}](/forum/ext/geomar/texintegr/latexrender/pictures/2874e6f835c7bf10a0cdeeb4ca8a321c.png) .
.Επίσης
 .Τελικά
.Τελικά  .
.Μέχρι εδώ έχω φτάσει,θα ακολουθήσουν και τα υπόλοιπα 2.
Γιώργος Γαβριλόπουλος
Re: Μαθηματικά κατεύθυνσης 2015
Θέμα Γ.
Γ.1 Η συνάρτηση είναι παραγωγίσιμη ως πηλίκο παραγωγίσιμων. .
.
Η παράγωγος δηλαδή είναι θετική εκτός από το σημείο .Άρα η συνάρτηση είναι γνησίως αύξουσα.
.Άρα η συνάρτηση είναι γνησίως αύξουσα.
Αφού είναι γνησίως αύξουσα το Σ.Τ. της είναι το .
.
Έχουμε .
.
Επίσης .
.
Άρα όπως θέλαμε.
όπως θέλαμε.
Γ.2 Ισχύει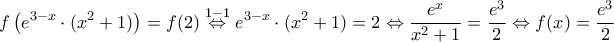 .
.
Αυτή η εξίσωση πράγματι έχει ακριβώς μια ρίζα αφού η είναι γνησίως αύξουσα άρα και
είναι γνησίως αύξουσα άρα και  κι επιπλέον
κι επιπλέον 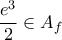 .
.
Άρα και η αρχική έχει μοναδική ρίζα όπως θέλαμε.
Γ.3 Για κάθε![\displaystyle{t\in [2x,4x]} \displaystyle{t\in [2x,4x]}](/forum/ext/geomar/texintegr/latexrender/pictures/b2323f894179bbd6d66fcc0cd2823ab6.png) ισχύει
ισχύει 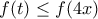 λόγω της μονοτονίας (σημειώστε ότι
λόγω της μονοτονίας (σημειώστε ότι  ).
).
Άρα![\displaystyle{\int_{2x}^{4x} f(t)dt\leq \int_{2x}^{4x} f(4x)dt=f(4x)\int_{2x}^{4x} 1dt=f(4x)[t]_{2x}^{4x}=2xf(4x)} \displaystyle{\int_{2x}^{4x} f(t)dt\leq \int_{2x}^{4x} f(4x)dt=f(4x)\int_{2x}^{4x} 1dt=f(4x)[t]_{2x}^{4x}=2xf(4x)}](/forum/ext/geomar/texintegr/latexrender/pictures/e61ba73c09ab01bbf94d80fac2c062d9.png) .
.
Επειδή η ισότητα δεν ισχύει για κάθε
δεν ισχύει για κάθε ![\displaystyle{t\in [2x,4x]} \displaystyle{t\in [2x,4x]}](/forum/ext/geomar/texintegr/latexrender/pictures/b2323f894179bbd6d66fcc0cd2823ab6.png) αλλά μόνο για ένα,η ανισότητα είναι γνήσια.
αλλά μόνο για ένα,η ανισότητα είναι γνήσια.
Γ.4 Για ισχύει
ισχύει  .
.
Αυτή για ισχύει αφού
ισχύει αφού  λόγω της μονοτονίας.Άρα η
λόγω της μονοτονίας.Άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  .
.
Επίσης αφού η
αφού η  είναι συνεχής.
είναι συνεχής.
Άρα η είναι και συνεχής στο
είναι και συνεχής στο  άρα είναι γνησίως αύξουσα σε όλο το
άρα είναι γνησίως αύξουσα σε όλο το  .
.
Edit:Τυπογραφικό στο τέλος.
Γ.1 Η συνάρτηση είναι παραγωγίσιμη ως πηλίκο παραγωγίσιμων.
 .
.Η παράγωγος δηλαδή είναι θετική εκτός από το σημείο
 .Άρα η συνάρτηση είναι γνησίως αύξουσα.
.Άρα η συνάρτηση είναι γνησίως αύξουσα.Αφού είναι γνησίως αύξουσα το Σ.Τ. της είναι το
 .
.Έχουμε
 .
.Επίσης
 .
.Άρα
 όπως θέλαμε.
όπως θέλαμε.Γ.2 Ισχύει
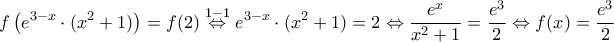 .
.Αυτή η εξίσωση πράγματι έχει ακριβώς μια ρίζα αφού η
 είναι γνησίως αύξουσα άρα και
είναι γνησίως αύξουσα άρα και  κι επιπλέον
κι επιπλέον 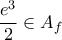 .
.Άρα και η αρχική έχει μοναδική ρίζα όπως θέλαμε.
Γ.3 Για κάθε
![\displaystyle{t\in [2x,4x]} \displaystyle{t\in [2x,4x]}](/forum/ext/geomar/texintegr/latexrender/pictures/b2323f894179bbd6d66fcc0cd2823ab6.png) ισχύει
ισχύει 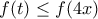 λόγω της μονοτονίας (σημειώστε ότι
λόγω της μονοτονίας (σημειώστε ότι  ).
).Άρα
![\displaystyle{\int_{2x}^{4x} f(t)dt\leq \int_{2x}^{4x} f(4x)dt=f(4x)\int_{2x}^{4x} 1dt=f(4x)[t]_{2x}^{4x}=2xf(4x)} \displaystyle{\int_{2x}^{4x} f(t)dt\leq \int_{2x}^{4x} f(4x)dt=f(4x)\int_{2x}^{4x} 1dt=f(4x)[t]_{2x}^{4x}=2xf(4x)}](/forum/ext/geomar/texintegr/latexrender/pictures/e61ba73c09ab01bbf94d80fac2c062d9.png) .
.Επειδή η ισότητα
 δεν ισχύει για κάθε
δεν ισχύει για κάθε ![\displaystyle{t\in [2x,4x]} \displaystyle{t\in [2x,4x]}](/forum/ext/geomar/texintegr/latexrender/pictures/b2323f894179bbd6d66fcc0cd2823ab6.png) αλλά μόνο για ένα,η ανισότητα είναι γνήσια.
αλλά μόνο για ένα,η ανισότητα είναι γνήσια.Γ.4 Για
 ισχύει
ισχύει  .
.Αυτή για
 ισχύει αφού
ισχύει αφού  λόγω της μονοτονίας.Άρα η
λόγω της μονοτονίας.Άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  .
.Επίσης
 αφού η
αφού η  είναι συνεχής.
είναι συνεχής.Άρα η
 είναι και συνεχής στο
είναι και συνεχής στο  άρα είναι γνησίως αύξουσα σε όλο το
άρα είναι γνησίως αύξουσα σε όλο το  .
.Edit:Τυπογραφικό στο τέλος.
τελευταία επεξεργασία από gavrilos σε Δευ Μάιος 25, 2015 12:58 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Γιώργος Γαβριλόπουλος
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2015
Για το Δ3
Η συνάρτηση έχει παράγωγο
έχει παράγωγο  άρα είναι γνησίως αύξουσα στο
άρα είναι γνησίως αύξουσα στο  οπότε για
οπότε για  έχουμε
έχουμε  συνεπώς
συνεπώς  για
για 
Το όριο γράφεται:
![\displaystyle\lim_{x\to 0^{+}}\left[\dfrac{F(x)-F(0)}{x-0} x\ln{f(x)} \right] \displaystyle\lim_{x\to 0^{+}}\left[\dfrac{F(x)-F(0)}{x-0} x\ln{f(x)} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/045531fbd00a84e3c4adb8ed849fedff.png) όπου
όπου  η οποία είναι παραγωγίσιμη με
η οποία είναι παραγωγίσιμη με 
Όμως
και επίσης
διότι
Η συνάρτηση
 έχει παράγωγο
έχει παράγωγο  άρα είναι γνησίως αύξουσα στο
άρα είναι γνησίως αύξουσα στο  οπότε για
οπότε για  έχουμε
έχουμε  συνεπώς
συνεπώς  για
για 
Το όριο γράφεται:
![\displaystyle\lim_{x\to 0^{+}}\left[\dfrac{F(x)-F(0)}{x-0} x\ln{f(x)} \right] \displaystyle\lim_{x\to 0^{+}}\left[\dfrac{F(x)-F(0)}{x-0} x\ln{f(x)} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/045531fbd00a84e3c4adb8ed849fedff.png) όπου
όπου  η οποία είναι παραγωγίσιμη με
η οποία είναι παραγωγίσιμη με 
Όμως

και επίσης

διότι

Αλέξανδρος Συγκελάκης
-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
Re: Μαθηματικά κατεύθυνσης 2015
Mια άλλη προσέγγιση από την ωραία και άμεση του Γιώργου στο Β2α) είναι να θεωρήσουμε πότε το κλάσμα  είναι πραγματικός (
είναι πραγματικός ( ) να φέρουμε το w με πράξεις στη μορφή
) να φέρουμε το w με πράξεις στη μορφή  (όπου
(όπου  ) οπότε αρκεί
) οπότε αρκεί  δηλαδή μετά από πράξεις
δηλαδή μετά από πράξεις  που ισχύει λόγω του πρώτου ερωτήματος.
που ισχύει λόγω του πρώτου ερωτήματος.
Καλή επιτυχία στους διαγωνιζόμενους!
 είναι πραγματικός (
είναι πραγματικός ( ) να φέρουμε το w με πράξεις στη μορφή
) να φέρουμε το w με πράξεις στη μορφή  (όπου
(όπου  ) οπότε αρκεί
) οπότε αρκεί  δηλαδή μετά από πράξεις
δηλαδή μετά από πράξεις  που ισχύει λόγω του πρώτου ερωτήματος.
που ισχύει λόγω του πρώτου ερωτήματος.Καλή επιτυχία στους διαγωνιζόμενους!
Σημαντήρης Γιάννης
Re: Μαθηματικά κατεύθυνσης 2015
Φοβερή η λύση του Αλέξανδρου,ας δούμε κι άλλη μία.Πάντως είναι ερώτημα που η λύση δε φαίνεται με την πρώτη ματιά (  ).
).
 .
.
Τα όρια σε αριθμητή και παρονομαστή παρουσιάζουν απροσδιόριστες μορφές στις οποίες μπορούμε να χρησιμοποιήσουμε DLH.
Τα υπολογίζουμε ξεχωριστά.Έχουμε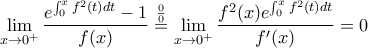 αφού
αφού  .
.
Επίσης .
.
Άρα το όριό μας παρουσιάζει τη μορφή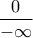 άρα ισούται με
άρα ισούται με  .
.
Ελπίζω να είναι σωστή.
 .
.Τα όρια σε αριθμητή και παρονομαστή παρουσιάζουν απροσδιόριστες μορφές στις οποίες μπορούμε να χρησιμοποιήσουμε DLH.
Τα υπολογίζουμε ξεχωριστά.Έχουμε
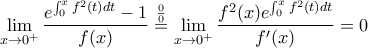 αφού
αφού  .
.Επίσης
 .
.Άρα το όριό μας παρουσιάζει τη μορφή
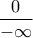 άρα ισούται με
άρα ισούται με  .
.Ελπίζω να είναι σωστή.
Γιώργος Γαβριλόπουλος
Re: Μαθηματικά κατεύθυνσης 2015
Αρκετός ο όγκος των ερωτημάτων αλλά τα περισσότερα από αυτά σχετικά "συνηθισμένα".Και μ' αυτό εννοώ ότι υπάρχουν παρόμοια σε όλα τα βιβλία τα οποία χρησιμοποιούν οι μαθητές στην προετοιμασία τους.
Θα ήθελα να σχολιάσω τα δύο τελευταία ερωτήματα του διαγωνίσματος (αυτά που πιστεύω θα χαρακτηριστούν ως δύσκολα από την πλειοψηφία).Η δυσκολία βρίσκεται,όχι στην εύρεση του τρόπου λύσης αλλά στην εύρεση του τρόπου εφαρμογής γνωστών τεχνικών.Και στα δύο δηλαδή γνωρίζουμε εξ' αρχής ποια τεχνική θα χρησιμοποιήσουμε (De' L Hospital και Bolzano αντίστοιχα) όμως η πολυπλοκότητα των εκφράσεων μας δυσκολεύει στον τρόπο εφαρμογής.
Άλλη μια παρατήρηση είναι ότι το Θ.Μ.Τ. και το Rolle απουσιάζουν από το διαγώνισμα.
Καλά αποτελέσματα σε όλους τους υποψηφίους!
Θα ήθελα να σχολιάσω τα δύο τελευταία ερωτήματα του διαγωνίσματος (αυτά που πιστεύω θα χαρακτηριστούν ως δύσκολα από την πλειοψηφία).Η δυσκολία βρίσκεται,όχι στην εύρεση του τρόπου λύσης αλλά στην εύρεση του τρόπου εφαρμογής γνωστών τεχνικών.Και στα δύο δηλαδή γνωρίζουμε εξ' αρχής ποια τεχνική θα χρησιμοποιήσουμε (De' L Hospital και Bolzano αντίστοιχα) όμως η πολυπλοκότητα των εκφράσεων μας δυσκολεύει στον τρόπο εφαρμογής.
Άλλη μια παρατήρηση είναι ότι το Θ.Μ.Τ. και το Rolle απουσιάζουν από το διαγώνισμα.
Καλά αποτελέσματα σε όλους τους υποψηφίους!
Γιώργος Γαβριλόπουλος
-
nikolaos p.
- Δημοσιεύσεις: 277
- Εγγραφή: Δευ Φεβ 14, 2011 11:44 pm
Re: Μαθηματικά κατεύθυνσης 2015
Ωραία τα θέματα, έχουν και εύκολα ερωτήματα και κάποια δυσκολότερα, που θα κάνουν τη διαφορά! Ίσως όμως τα δυσκολότερα θα μπορούσαν να είναι πιο λίγα.
τελευταία επεξεργασία από nikolaos p. σε Τρί Μάιος 26, 2015 6:38 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13275
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Μαθηματικά κατεύθυνσης 2015
Για το Δ3, όσοι είχαν υπόψη τους την άσκηση  της παραγράφου
της παραγράφου  του σχολικού βιβλίου, θα πήγε αμέσως το μυαλό τους να διαιρέσουν και να πολλαπλασιάσουν με
του σχολικού βιβλίου, θα πήγε αμέσως το μυαλό τους να διαιρέσουν και να πολλαπλασιάσουν με  .
.
 της παραγράφου
της παραγράφου  του σχολικού βιβλίου, θα πήγε αμέσως το μυαλό τους να διαιρέσουν και να πολλαπλασιάσουν με
του σχολικού βιβλίου, θα πήγε αμέσως το μυαλό τους να διαιρέσουν και να πολλαπλασιάσουν με  .
.Re: Μαθηματικά κατεύθυνσης 2015
Τοgavrilos έγραψε:
Άλλη μια παρατήρηση είναι ότι το Θ.Μ.Τ. και το Rolle απουσιάζουν από το διαγώνισμα.
 βγαίνει και με ΘΜΤ
βγαίνει και με ΘΜΤ- ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
- Επιμελητής
- Δημοσιεύσεις: 4658
- Εγγραφή: Κυρ Μαρ 13, 2011 9:11 pm
- Τοποθεσία: Βρυξέλλες
Re: Μαθηματικά κατεύθυνσης 2015
Δ1. Είναι ![f'\left( x \right) \cdot \left[ {{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}}} \right] = 2 \Leftrightarrow {e^{f\left( x \right)}} \cdot f'\left( x \right) + {e^{ - f\left( x \right)}} \cdot f'\left( x \right) = 2 \Leftrightarrow f'\left( x \right) \cdot \left[ {{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}}} \right] = 2 \Leftrightarrow {e^{f\left( x \right)}} \cdot f'\left( x \right) + {e^{ - f\left( x \right)}} \cdot f'\left( x \right) = 2 \Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/d049013f856ef71345bcd9897f60d08e.png)
 .
.
Για η σχέση
η σχέση  γίνεται
γίνεται 
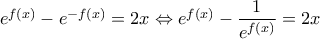


 , για κάθε
, για κάθε  .
.
Θεωρούμε τη συνάρτηση . Επειδή
. Επειδή  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  (από την υπόθεση) θα είναι και συνεχής και επειδή
(από την υπόθεση) θα είναι και συνεχής και επειδή
η συνάρτηση είναι συνεχής στο
είναι συνεχής στο  άρα και στα
άρα και στα  προκύπτει ότι η
προκύπτει ότι η  θα είναι συνεχής στο
θα είναι συνεχής στο 
και με την συνεχή στο
συνεχή στο  (ταυτοτική) προκύπτει ότι η
(ταυτοτική) προκύπτει ότι η  θα είναι συνεχής στο
θα είναι συνεχής στο  (διαφορά συνεχών)
(διαφορά συνεχών)
και με για κάθε
για κάθε  (όπως προκύπτει από τη σχέση
(όπως προκύπτει από τη σχέση  ) αυτή θα διατηρεί το πρόσημό της στο
) αυτή θα διατηρεί το πρόσημό της στο  και με
και με 
για κάθε από την
από την  θα έχουμε:
θα έχουμε:


(αφού για κάθε
για κάθε  ) οπότε από
) οπότε από

 .
.
Δ2. α) Από τη σχέση![f'\left( x \right) \cdot \left[ {{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}}} \right] = 2\mathop \Rightarrow \limits^{{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}} > 0,\forall x \in R} f'\left( x \right) \cdot \left[ {{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}}} \right] = 2\mathop \Rightarrow \limits^{{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}} > 0,\forall x \in R}](/forum/ext/geomar/texintegr/latexrender/pictures/defa4b4b0d9d8577dae2d39fcf79dbc6.png)
 για κάθε
για κάθε 
οπότε η είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και από τον τύπο
και από τον τύπο  προκύπτει ότι η
προκύπτει ότι η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  (... πράξεις με παραγωγίσιμες) με
(... πράξεις με παραγωγίσιμες) με



Είναι


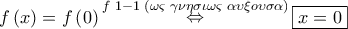
Για

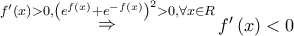 και με
και με
 συνεχή στο διάστημα
συνεχή στο διάστημα  επειδή είναι παραγωγίσιμη στο
επειδή είναι παραγωγίσιμη στο  (από την εκφώνηση) προκύπτει ότι η
(από την εκφώνηση) προκύπτει ότι η  θα είναι κοίλη στο διάστημα
θα είναι κοίλη στο διάστημα  και
και
για


 και με
και με  συνεχή στο διάστημα
συνεχή στο διάστημα ![\left( { - \infty ,0} \right] \left( { - \infty ,0} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/b8ca05bb5238a874a6434ebf5713206d.png) (επειδή είναι παραγωγίσιμη στο
(επειδή είναι παραγωγίσιμη στο  (από την εκφώνηση) )
(από την εκφώνηση) )
προκύπτει ότι η είναι κυρτή στο διάστημα
είναι κυρτή στο διάστημα ![\left( { - \infty ,0} \right] \left( { - \infty ,0} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/b8ca05bb5238a874a6434ebf5713206d.png) το δε σημείο
το δε σημείο  είναι σημείο καμπής
είναι σημείο καμπής
της γραφικής της παράστασης (αφού και εκατέρωθεν του μηδενός αλλάζει το πρόσημο της δεύτερης παραγώγου).
και εκατέρωθεν του μηδενός αλλάζει το πρόσημο της δεύτερης παραγώγου).
β) Αν είναι το ζητούμενο εμβαδόν τότε θα έχουμε:
είναι το ζητούμενο εμβαδόν τότε θα έχουμε:  .
.
Θεωρούμε τη συνάρτηση , η οποία είναι συνεχής (διαφορά συνεχών) στο διάστημα
, η οποία είναι συνεχής (διαφορά συνεχών) στο διάστημα ![\left[ {0,1} \right] \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/8c0948bf2a66db5ceb6d006ef91282d7.png) , παραγωγίσιμη στο
, παραγωγίσιμη στο  (διαφορά παραγωγισίμων)
(διαφορά παραγωγισίμων)
με
 για κάθε
για κάθε 
(αφού για είναι
είναι  , οπότε η
, οπότε η 
είναι γνησίως φθίνουσα στο![\left[ {0,1} \right] \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/8c0948bf2a66db5ceb6d006ef91282d7.png) και με
και με  προκύπτει ότι
προκύπτει ότι 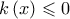 , για κάθε
, για κάθε ![x \in \left[ {0,1} \right] x \in \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/b35e5438585f851ee324bacf1b792d90.png) ,
,
οπότε από την έχουμε ότι:
έχουμε ότι: 
![= \left[ {\dfrac{{{x^2}}}{2}} \right]_0^1 - \left( {\left[ {xf\left( x \right)} \right]_0^1 - \int\limits_0^1 {xf'\left( x \right)dx} } \right) = = \left[ {\dfrac{{{x^2}}}{2}} \right]_0^1 - \left( {\left[ {xf\left( x \right)} \right]_0^1 - \int\limits_0^1 {xf'\left( x \right)dx} } \right) =](/forum/ext/geomar/texintegr/latexrender/pictures/8f931e2fdf1c5a2b2c305f7267127424.png)
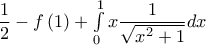
![= \dfrac{1}{2} - \ln \left( {1 + \sqrt 2 } \right) + \left[ {\sqrt {{x^2} + 1} } \right]_0^1 = = \dfrac{1}{2} - \ln \left( {1 + \sqrt 2 } \right) + \left[ {\sqrt {{x^2} + 1} } \right]_0^1 =](/forum/ext/geomar/texintegr/latexrender/pictures/415ea1a5e173b3b0c7abdbcc15e47d07.png)

 .
.
Δ3, Με συνεχή στο
συνεχή στο  (δύναμη συνεχούς και
(δύναμη συνεχούς και  προκύπτει ότι η
προκύπτει ότι η  είναι μια παράγουσα της
είναι μια παράγουσα της  στο
στο  άρα συνεχής
άρα συνεχής
και με συνεχή στο
συνεχή στο  προκύπτει ότι η
προκύπτει ότι η  είναι συνεχής στο
είναι συνεχής στο  άρα και στο μηδέν
άρα και στο μηδέν
οπότε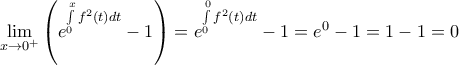 και
και
![\mathop {\lim }\limits_{x \to {0^ + }} \left[ {\ln \left| {f\left( x \right)} \right|} \right]\mathop = \limits^{f\left( x \right) > 0,\gamma \iota \alpha \,\,x > 0} \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\ln f\left( x \right)} \right] \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\ln \left| {f\left( x \right)} \right|} \right]\mathop = \limits^{f\left( x \right) > 0,\gamma \iota \alpha \,\,x > 0} \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\ln f\left( x \right)} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/292bad196284b8b4cffc77e103a387b6.png)
 .
.
Έτσι έχουμε:![\mathop {\lim }\limits_{x \to {0^ + }} \left[ {\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right) \cdot \ln \left| {f\left( x \right)} \right|} \right] = \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\dfrac{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1}}{{\dfrac{1}{{\ln f\left( x \right)}}}}} \right] \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right) \cdot \ln \left| {f\left( x \right)} \right|} \right] = \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\dfrac{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1}}{{\dfrac{1}{{\ln f\left( x \right)}}}}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/77910ae60b57004853274951c22e4fc4.png) και με τις συναρτήσεις
και με τις συναρτήσεις 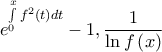
παραγωγίσιμες είναι

![\mathop {\lim }\limits_{x \to {0^ + }} \left[ { - \dfrac{{f'\left( x \right)}}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }}}} \cdot \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}} \right] \mathop {\lim }\limits_{x \to {0^ + }} \left[ { - \dfrac{{f'\left( x \right)}}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }}}} \cdot \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/22e679574267930dd100f640295420cd.png) .
.
Είναι και
και
![\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}\mathop = \limits_{De\,\,L'Hospital}^{\dfrac{0}{0}} \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left[ {{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}} \right]}^\prime }}}{{{{\left( {{f^3}\left( x \right)} \right)}^\prime }}} \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}\mathop = \limits_{De\,\,L'Hospital}^{\dfrac{0}{0}} \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left[ {{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}} \right]}^\prime }}}{{{{\left( {{f^3}\left( x \right)} \right)}^\prime }}}](/forum/ext/geomar/texintegr/latexrender/pictures/060e9ed03f6fbd2828595999a4f5abb7.png)



 . Οπότε τελικά για το ζητούμενο όριο
. Οπότε τελικά για το ζητούμενο όριο
(από όρια και πράξεις) έχουμε :![\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left( {\ln f\left( x \right)} \right)}^\prime }}}{{{{\left( {\dfrac{1}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1}}} \right)}^\prime }}} = \ldots \mathop {\lim }\limits_{x \to {0^ + }} \left[ { - \dfrac{{f'\left( x \right)}}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }}}} \cdot \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}} \right] = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left( {\ln f\left( x \right)} \right)}^\prime }}}{{{{\left( {\dfrac{1}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1}}} \right)}^\prime }}} = \ldots \mathop {\lim }\limits_{x \to {0^ + }} \left[ { - \dfrac{{f'\left( x \right)}}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }}}} \cdot \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/1e0c4f237e3676f8a3465120a9ffb24f.png)
 .
.
Στάθης
Υ.ΣΓια το Δ4 ταυτίζομαι με τον Αλέξανδρο (Συγκελάκη) και νομίζω ότι είναι η πιο ενδεδειγμένη αντιμετώπιση
![f'\left( x \right) \cdot \left[ {{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}}} \right] = 2 \Leftrightarrow {e^{f\left( x \right)}} \cdot f'\left( x \right) + {e^{ - f\left( x \right)}} \cdot f'\left( x \right) = 2 \Leftrightarrow f'\left( x \right) \cdot \left[ {{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}}} \right] = 2 \Leftrightarrow {e^{f\left( x \right)}} \cdot f'\left( x \right) + {e^{ - f\left( x \right)}} \cdot f'\left( x \right) = 2 \Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/d049013f856ef71345bcd9897f60d08e.png)
 .
.Για
 η σχέση
η σχέση  γίνεται
γίνεται 
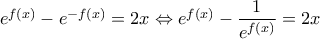


 , για κάθε
, για κάθε  .
.Θεωρούμε τη συνάρτηση
 . Επειδή
. Επειδή  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  (από την υπόθεση) θα είναι και συνεχής και επειδή
(από την υπόθεση) θα είναι και συνεχής και επειδή η συνάρτηση
 είναι συνεχής στο
είναι συνεχής στο  άρα και στα
άρα και στα  προκύπτει ότι η
προκύπτει ότι η  θα είναι συνεχής στο
θα είναι συνεχής στο 
και με την
 συνεχή στο
συνεχή στο  (ταυτοτική) προκύπτει ότι η
(ταυτοτική) προκύπτει ότι η  θα είναι συνεχής στο
θα είναι συνεχής στο  (διαφορά συνεχών)
(διαφορά συνεχών) και με
 για κάθε
για κάθε  (όπως προκύπτει από τη σχέση
(όπως προκύπτει από τη σχέση  ) αυτή θα διατηρεί το πρόσημό της στο
) αυτή θα διατηρεί το πρόσημό της στο  και με
και με 
για κάθε
 από την
από την  θα έχουμε:
θα έχουμε: 

(αφού
 για κάθε
για κάθε  ) οπότε από
) οπότε από 
 .
.Δ2. α) Από τη σχέση
![f'\left( x \right) \cdot \left[ {{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}}} \right] = 2\mathop \Rightarrow \limits^{{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}} > 0,\forall x \in R} f'\left( x \right) \cdot \left[ {{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}}} \right] = 2\mathop \Rightarrow \limits^{{e^{f\left( x \right)}} + {e^{ - f\left( x \right)}} > 0,\forall x \in R}](/forum/ext/geomar/texintegr/latexrender/pictures/defa4b4b0d9d8577dae2d39fcf79dbc6.png)
 για κάθε
για κάθε 
οπότε η
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και από τον τύπο
και από τον τύπο  προκύπτει ότι η
προκύπτει ότι η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  (... πράξεις με παραγωγίσιμες) με
(... πράξεις με παραγωγίσιμες) με 


Είναι



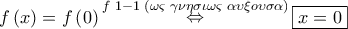
Για


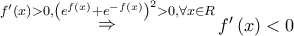 και με
και με  συνεχή στο διάστημα
συνεχή στο διάστημα  επειδή είναι παραγωγίσιμη στο
επειδή είναι παραγωγίσιμη στο  (από την εκφώνηση) προκύπτει ότι η
(από την εκφώνηση) προκύπτει ότι η  θα είναι κοίλη στο διάστημα
θα είναι κοίλη στο διάστημα  και
και για



 και με
και με  συνεχή στο διάστημα
συνεχή στο διάστημα ![\left( { - \infty ,0} \right] \left( { - \infty ,0} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/b8ca05bb5238a874a6434ebf5713206d.png) (επειδή είναι παραγωγίσιμη στο
(επειδή είναι παραγωγίσιμη στο  (από την εκφώνηση) )
(από την εκφώνηση) ) προκύπτει ότι η
 είναι κυρτή στο διάστημα
είναι κυρτή στο διάστημα ![\left( { - \infty ,0} \right] \left( { - \infty ,0} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/b8ca05bb5238a874a6434ebf5713206d.png) το δε σημείο
το δε σημείο  είναι σημείο καμπής
είναι σημείο καμπής της γραφικής της παράστασης (αφού
 και εκατέρωθεν του μηδενός αλλάζει το πρόσημο της δεύτερης παραγώγου).
και εκατέρωθεν του μηδενός αλλάζει το πρόσημο της δεύτερης παραγώγου). β) Αν
 είναι το ζητούμενο εμβαδόν τότε θα έχουμε:
είναι το ζητούμενο εμβαδόν τότε θα έχουμε:  .
. Θεωρούμε τη συνάρτηση
 , η οποία είναι συνεχής (διαφορά συνεχών) στο διάστημα
, η οποία είναι συνεχής (διαφορά συνεχών) στο διάστημα ![\left[ {0,1} \right] \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/8c0948bf2a66db5ceb6d006ef91282d7.png) , παραγωγίσιμη στο
, παραγωγίσιμη στο  (διαφορά παραγωγισίμων)
(διαφορά παραγωγισίμων) με

 για κάθε
για κάθε 
(αφού για
 είναι
είναι  , οπότε η
, οπότε η 
είναι γνησίως φθίνουσα στο
![\left[ {0,1} \right] \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/8c0948bf2a66db5ceb6d006ef91282d7.png) και με
και με  προκύπτει ότι
προκύπτει ότι 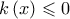 , για κάθε
, για κάθε ![x \in \left[ {0,1} \right] x \in \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/b35e5438585f851ee324bacf1b792d90.png) ,
,οπότε από την
 έχουμε ότι:
έχουμε ότι: 
![= \left[ {\dfrac{{{x^2}}}{2}} \right]_0^1 - \left( {\left[ {xf\left( x \right)} \right]_0^1 - \int\limits_0^1 {xf'\left( x \right)dx} } \right) = = \left[ {\dfrac{{{x^2}}}{2}} \right]_0^1 - \left( {\left[ {xf\left( x \right)} \right]_0^1 - \int\limits_0^1 {xf'\left( x \right)dx} } \right) =](/forum/ext/geomar/texintegr/latexrender/pictures/8f931e2fdf1c5a2b2c305f7267127424.png)
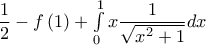
![= \dfrac{1}{2} - \ln \left( {1 + \sqrt 2 } \right) + \left[ {\sqrt {{x^2} + 1} } \right]_0^1 = = \dfrac{1}{2} - \ln \left( {1 + \sqrt 2 } \right) + \left[ {\sqrt {{x^2} + 1} } \right]_0^1 =](/forum/ext/geomar/texintegr/latexrender/pictures/415ea1a5e173b3b0c7abdbcc15e47d07.png)

 .
.Δ3, Με
 συνεχή στο
συνεχή στο  (δύναμη συνεχούς και
(δύναμη συνεχούς και  προκύπτει ότι η
προκύπτει ότι η  είναι μια παράγουσα της
είναι μια παράγουσα της  στο
στο  άρα συνεχής
άρα συνεχήςκαι με
 συνεχή στο
συνεχή στο  προκύπτει ότι η
προκύπτει ότι η  είναι συνεχής στο
είναι συνεχής στο  άρα και στο μηδέν
άρα και στο μηδέν οπότε
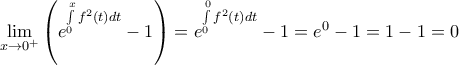 και
και ![\mathop {\lim }\limits_{x \to {0^ + }} \left[ {\ln \left| {f\left( x \right)} \right|} \right]\mathop = \limits^{f\left( x \right) > 0,\gamma \iota \alpha \,\,x > 0} \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\ln f\left( x \right)} \right] \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\ln \left| {f\left( x \right)} \right|} \right]\mathop = \limits^{f\left( x \right) > 0,\gamma \iota \alpha \,\,x > 0} \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\ln f\left( x \right)} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/292bad196284b8b4cffc77e103a387b6.png)
 .
.Έτσι έχουμε:
![\mathop {\lim }\limits_{x \to {0^ + }} \left[ {\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right) \cdot \ln \left| {f\left( x \right)} \right|} \right] = \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\dfrac{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1}}{{\dfrac{1}{{\ln f\left( x \right)}}}}} \right] \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right) \cdot \ln \left| {f\left( x \right)} \right|} \right] = \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\dfrac{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1}}{{\dfrac{1}{{\ln f\left( x \right)}}}}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/77910ae60b57004853274951c22e4fc4.png) και με τις συναρτήσεις
και με τις συναρτήσεις 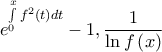
παραγωγίσιμες είναι


![\mathop {\lim }\limits_{x \to {0^ + }} \left[ { - \dfrac{{f'\left( x \right)}}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }}}} \cdot \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}} \right] \mathop {\lim }\limits_{x \to {0^ + }} \left[ { - \dfrac{{f'\left( x \right)}}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }}}} \cdot \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/22e679574267930dd100f640295420cd.png) .
.Είναι
 και
και ![\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}\mathop = \limits_{De\,\,L'Hospital}^{\dfrac{0}{0}} \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left[ {{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}} \right]}^\prime }}}{{{{\left( {{f^3}\left( x \right)} \right)}^\prime }}} \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}\mathop = \limits_{De\,\,L'Hospital}^{\dfrac{0}{0}} \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left[ {{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}} \right]}^\prime }}}{{{{\left( {{f^3}\left( x \right)} \right)}^\prime }}}](/forum/ext/geomar/texintegr/latexrender/pictures/060e9ed03f6fbd2828595999a4f5abb7.png)



 . Οπότε τελικά για το ζητούμενο όριο
. Οπότε τελικά για το ζητούμενο όριο(από όρια και πράξεις) έχουμε :
![\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left( {\ln f\left( x \right)} \right)}^\prime }}}{{{{\left( {\dfrac{1}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1}}} \right)}^\prime }}} = \ldots \mathop {\lim }\limits_{x \to {0^ + }} \left[ { - \dfrac{{f'\left( x \right)}}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }}}} \cdot \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}} \right] = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{{\left( {\ln f\left( x \right)} \right)}^\prime }}}{{{{\left( {\dfrac{1}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1}}} \right)}^\prime }}} = \ldots \mathop {\lim }\limits_{x \to {0^ + }} \left[ { - \dfrac{{f'\left( x \right)}}{{{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }}}} \cdot \dfrac{{{{\left( {{e^{\int\limits_0^x {{f^2}\left( t \right)dt} }} - 1} \right)}^2}}}{{{f^3}\left( x \right)}}} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/1e0c4f237e3676f8a3465120a9ffb24f.png)
 .
.Στάθης
Υ.ΣΓια το Δ4 ταυτίζομαι με τον Αλέξανδρο (Συγκελάκη) και νομίζω ότι είναι η πιο ενδεδειγμένη αντιμετώπιση
Τι περιμένετε λοιπόν ναρθεί , ποιόν καρτεράτε να σας σώσει.
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
-
zoumero_mpifteki
- Δημοσιεύσεις: 7
- Εγγραφή: Κυρ Οκτ 26, 2014 10:17 am
Re: Μαθηματικά κατεύθυνσης 2015
Μια ερώτηση. Αριθμητικό λάθος στον υπολογισμό του Δ2(β), με πλήρη αιτιολόγηση προσήμων της  και μη αιτιολόγηση προσήμων στα
και μη αιτιολόγηση προσήμων στα  και
και  της συνάρτησης που ορίζουμε εμείς στο Δ4 για να εφαρμόσουμε Bolzano, πόσο περίπου κόβουν;
της συνάρτησης που ορίζουμε εμείς στο Δ4 για να εφαρμόσουμε Bolzano, πόσο περίπου κόβουν;
 και μη αιτιολόγηση προσήμων στα
και μη αιτιολόγηση προσήμων στα  και
και  της συνάρτησης που ορίζουμε εμείς στο Δ4 για να εφαρμόσουμε Bolzano, πόσο περίπου κόβουν;
της συνάρτησης που ορίζουμε εμείς στο Δ4 για να εφαρμόσουμε Bolzano, πόσο περίπου κόβουν;
τελευταία επεξεργασία από matha σε Δευ Μάιος 25, 2015 7:33 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λόγος: Τονισμός κειμένου και διόρθωση LaTeX!
Λόγος: Τονισμός κειμένου και διόρθωση LaTeX!
Δημήτρης Π.
Re: Μαθηματικά κατεύθυνσης 2015
Το Γ3 με ΘΜΤ στο ![[2χ, 4χ] [2χ, 4χ]](/forum/ext/geomar/texintegr/latexrender/pictures/31529d19bf27f79c25b041ab6931dad0.png) και μετά με μονοτονία της
και μετά με μονοτονία της ?
?
![[2χ, 4χ] [2χ, 4χ]](/forum/ext/geomar/texintegr/latexrender/pictures/31529d19bf27f79c25b041ab6931dad0.png) και μετά με μονοτονία της
και μετά με μονοτονία της ?
?Know how to solve every problem that has been solved.
--- Richard Feynman
--- Richard Feynman
Re: Μαθηματικά κατεύθυνσης 2015
Δ2. β) Για το πρόσημο της διαφοράς. Παρατηρώ ότι η  είναι εφαπτομένη της
είναι εφαπτομένη της  στο
στο  και αφού η
και αφού η  είναι κοίλη, βρίσκεται κάτω από την εφαπτομένη.
είναι κοίλη, βρίσκεται κάτω από την εφαπτομένη.
edit (μόλις διαπίστωσα ότι έχει σχολιαστεί παραπάνω)
 είναι εφαπτομένη της
είναι εφαπτομένη της  στο
στο  και αφού η
και αφού η  είναι κοίλη, βρίσκεται κάτω από την εφαπτομένη.
είναι κοίλη, βρίσκεται κάτω από την εφαπτομένη.edit (μόλις διαπίστωσα ότι έχει σχολιαστεί παραπάνω)
τελευταία επεξεργασία από matha σε Δευ Μάιος 25, 2015 7:34 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Λόγος: Διόρθωση LaTeX!
Λόγος: Διόρθωση LaTeX!
Η ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΔΕΝ ΜΠΟΡΕΙ ΝΑ ΚΕΡΔΙΣΕΙ ΤΗ ΦΥΣΙΚΗ ΗΛΙΘΙΟΤΗΤΑ - ΑΡΚΑΣ
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
