Μαθηματικά κατεύθυνσης 2015
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: Μαθηματικά κατεύθυνσης 2015
Κύριε Στεργίου μιας και αύριο θα ξεκινήσετε τις διορθώσεις θα μπορούσατε μήπως να μας αναφέρετε μερικά στοιχεία το βράδυ; π.χ "διόρθωσα 20 γραπτά...τα 10 ήταν κάτω από τη βάση 7 μέχρι 15 και 3 20αρια???προς φιλοσοφικής συζήτησης και μόνο...
Τονισμός κειμένου
Τονισμός κειμένου
τελευταία επεξεργασία από matha σε Τρί Μάιος 26, 2015 10:35 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λόγος: Τονισμός κειμένου!
Λόγος: Τονισμός κειμένου!
- S.E.Louridas
- Δημοσιεύσεις: 5954
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2015
Και μόνο για λόγους πλουραλισμού (σε αυτό το πνεύμα θα πρέπει να δίνουμε τρόπους διαφορετικής νοοτροπίας, ώστε να εξυπηρετούμε και την υποκειμενικότητα των διαγωνιζομένων δηλαδή τι τους ταιριάζει) ας δούμε και έναν άλλο τρόπο για την εύρεση του Πεδίου τιμών της 
Καταρχάς παρατηρούμε ότι Θα πρέπει τώρα για τον τυχόντα θετικό
Θα πρέπει τώρα για τον τυχόντα θετικό 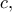 να υπάρχει πραγματικός
να υπάρχει πραγματικός  ώστε
ώστε  Για την
Για την 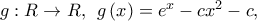 έστω ότι
έστω ότι  Τότε κατά μείζονα λόγο θα είχαμε και
Τότε κατά μείζονα λόγο θα είχαμε και  άρα θα είχαμε
άρα θα είχαμε  που είναι άτοπο. Θα υπάρχει λοιπόν πραγματικός
που είναι άτοπο. Θα υπάρχει λοιπόν πραγματικός  τέτοιος που
τέτοιος που  Αν τώρα ίσχυε
Αν τώρα ίσχυε  τότε για
τότε για 
 θα είχαμε
θα είχαμε  που είναι άτοπο. Άρα θα υπάρχει πραγματικός
που είναι άτοπο. Άρα θα υπάρχει πραγματικός  Από τις
Από τις  παίρνουμε το ζητούμενο.
παίρνουμε το ζητούμενο.

Καταρχάς παρατηρούμε ότι
 Θα πρέπει τώρα για τον τυχόντα θετικό
Θα πρέπει τώρα για τον τυχόντα θετικό 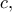 να υπάρχει πραγματικός
να υπάρχει πραγματικός  ώστε
ώστε  Για την
Για την 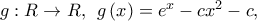 έστω ότι
έστω ότι  Τότε κατά μείζονα λόγο θα είχαμε και
Τότε κατά μείζονα λόγο θα είχαμε και  άρα θα είχαμε
άρα θα είχαμε  που είναι άτοπο. Θα υπάρχει λοιπόν πραγματικός
που είναι άτοπο. Θα υπάρχει λοιπόν πραγματικός  τέτοιος που
τέτοιος που  Αν τώρα ίσχυε
Αν τώρα ίσχυε  τότε για
τότε για 
 θα είχαμε
θα είχαμε  που είναι άτοπο. Άρα θα υπάρχει πραγματικός
που είναι άτοπο. Άρα θα υπάρχει πραγματικός  Από τις
Από τις  παίρνουμε το ζητούμενο.
παίρνουμε το ζητούμενο.
τελευταία επεξεργασία από S.E.Louridas σε Τρί Μάιος 26, 2015 7:09 pm, έχει επεξεργασθεί 2 φορές συνολικά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
- chris_gatos
- Επιμελητής
- Δημοσιεύσεις: 6962
- Εγγραφή: Κυρ Δεκ 21, 2008 9:03 pm
- Τοποθεσία: Ανθούπολη
Re: Μαθηματικά κατεύθυνσης 2015
Επειδή έχω καταλάβει καλά πως ο Νίκος ποτέ δε μιλάει τυχαία θέλω να πω πως το τελευταίο ερώτημα του θέματος Δ μου έφερεnikoszan έγραψε:Μια άσκηση(ιδέα για μελλοντικης μορφής θέμα?) αφιερωμένη στους φίλους θεματοδότες ,που τόσο πολύ έχουν κατακριθεί.(ΧΡΟΝΟΣ ΛΥΣΗΣ 15min με σχολικά μαθηματικά και με πλήρη διατύπωση)
Έστω η τρεις φορές παραγωγίσιμη συνάρτηση,για την οποία ισχύει :
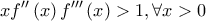
και το σημείοβρίσκεται κάτω απο το μέσο του ευθ. τμήματος
,όπου
και
.
Να βρεθεί το όριο :.
Ερώτηση 1 : Είναι επαρκής ο χρόνος ?
Ερώτηση 2 :Έχουν διδαχθεί οι μαθητές και όχι μόνο τέτοιας μορφής θέμα.
Ερώτηση 3:Μήπως είμαι αρκετά κακός θεματοδότης(ισχυρίζομαι οτι δεν έχω τέτοια πρόθεση)
ΣΧΟΛΙΟ1:Για να μην παρεξηγηθώ , τα θέματα απο μαθηματικη άποψη είναι άψογα και ειναι σχεδόν ταυτόσημα της νοοτροπίας με την οποία προπονώ τους μαθητές.
Θα σχολιάσω όμως μόνο ένα(υπάρχουν και άλλα ) : ότι ο χρόνος των τριών ωρών δεν έφτανε να απαντηθούν με πλήρη διατύπωση τα θέματα αυτά απο τους
περισσότερους μαθητές και οχι μόνο (ΠΡΟΤΕΙΝΟΜΕΝΟΣ ΧΡΟΝΟΣ:(ΧΡΟΝΟΣ ΚΑΘΗΓΗΤΗ ΛΥΤΗ ΜΕ ΠΛΗΡΗ ΔΙΑΤΥΠΩΣΗ )Χ3)
ΣΧΟΛΙΟ2Αν ο χρονος των 15min δεν φτάνει ,για να απαντηθεί το προτεινόμενο θέμα, δινεται επι πλεον χρόνος 5 min.
ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ: ΟΤΑΝ ΠΕΦΤΟΥΜΕ ΠΡΕΠΕΙ ΝΑ ΒΡΟΥΜΕ ΤΗΝ ΔΥΝΑΜΗ ΝΑ ΣΗΚΩΘΟΥΜΕ! ΚΑΛΗ ΕΠΙΤΥΧΙΑ!!
Ν.Ζ.
κατευθείαν στο μυαλό τα ερωτήματα που θέτει στο φόρουμ "Ολοκλήρωμα και διάταξη".
Πηγαίνοντας πίσω, στα παλιά του φόρουμ, βρήκα --->αυτό.
Αξίζει να διαβάσετε τους προβληματισμούς του αείμνηστου Κώστα Ζερβού. Το ίδιο περίπου ισχυρίζεται και ο Νίκος.
Χρήστος Κυριαζής
- Λάμπρος Μπαλός
- Δημοσιεύσεις: 984
- Εγγραφή: Τρί Αύγ 13, 2013 12:21 pm
- Τοποθεσία: Τρίκαλα
Re: Μαθηματικά κατεύθυνσης 2015
Δεν ανέφερα κάτι μέχρι στιγμής, περιμένοντας βεβαίως να μιλήσουν οι παλαιότεροι αυτής της παρέας.
Θα αναφέρω μόνο τα σχόλια δύο ανθρώπων.
Ο πρώτος είναι ο τολάσο που μόλις είδε τα θέματα μου έγραψε.. "μου θυμίζουν Ζανταρίδη"
Ο δεύτερος είναι ένας μαθητής μου που κουράστηκε πολύ μεσα στη χρονιά και μόλις έφτασε στο φροντιστήριο, πριν καν μου πει πώς τα πήγε (τα έγραψε όλα στο μεταξύ το θηρίο) , τον ρώτησα : "έλα πες,σου θυμίζουν κάτι;". Η απάντηση ήρθε χωρίς δεύτερη σκέψη.
Μόνο να πω, σε δομή και σε ομορφιά οι θεματοδότες δεν τον φτάνουν τον κύριο Νίκο.
Υγ.. Το μεγάλο μας καμάρι , το μεγάλο μας στήριγμα , είναι η Γλώσσα μας. Αν το χάσουμε, χαθήκαμε. Να διαβάζουμε όσο μπορούμε.
...μνημονεύετε Διονύσιο Σολωμό και μνημονεύετε Αλέξανδρο Παπαδιαμάντη. Πράγματι είναι η λαλιά που δεν ξέρει από ψέμα. Σαν τα Μαθηματικά ένα πράμα..
Θα αναφέρω μόνο τα σχόλια δύο ανθρώπων.
Ο πρώτος είναι ο τολάσο που μόλις είδε τα θέματα μου έγραψε.. "μου θυμίζουν Ζανταρίδη"
Ο δεύτερος είναι ένας μαθητής μου που κουράστηκε πολύ μεσα στη χρονιά και μόλις έφτασε στο φροντιστήριο, πριν καν μου πει πώς τα πήγε (τα έγραψε όλα στο μεταξύ το θηρίο) , τον ρώτησα : "έλα πες,σου θυμίζουν κάτι;". Η απάντηση ήρθε χωρίς δεύτερη σκέψη.
Μόνο να πω, σε δομή και σε ομορφιά οι θεματοδότες δεν τον φτάνουν τον κύριο Νίκο.
Υγ.. Το μεγάλο μας καμάρι , το μεγάλο μας στήριγμα , είναι η Γλώσσα μας. Αν το χάσουμε, χαθήκαμε. Να διαβάζουμε όσο μπορούμε.
...μνημονεύετε Διονύσιο Σολωμό και μνημονεύετε Αλέξανδρο Παπαδιαμάντη. Πράγματι είναι η λαλιά που δεν ξέρει από ψέμα. Σαν τα Μαθηματικά ένα πράμα..
Λάμπρος Μπαλός
lamprosbalos81@gmail.com
lamprosbalos81@gmail.com
Re: Μαθηματικά κατεύθυνσης 2015
Λάμπρος Μπαλός έγραψε:Δεν ανέφερα κάτι μέχρι στιγμής, περιμένοντας βεβαίως να μιλήσουν οι παλαιότεροι αυτής της παρέας.
Θα αναφέρω μόνο τα σχόλια δύο ανθρώπων.
Ο πρώτος είναι ο τολάσο που μόλις είδε τα θέματα μου έγραψε.. "μου θυμίζουν Ζανταρίδη"
Ο δεύτερος είναι ένας μαθητής μου που κουράστηκε πολύ μεσα στη χρονιά και μόλις έφτασε στο φροντιστήριο, πριν καν μου πει πώς τα πήγε (τα έγραψε όλα στο μεταξύ το θηρίο) , τον ρώτησα : "έλα πες,σου θυμίζουν κάτι;". Η απάντηση ήρθε χωρίς δεύτερη σκέψη.
Μόνο να πω, σε δομή και σε ομορφιά οι θεματοδότες δεν τον φτάνουν τον κύριο Νίκο.
Υγ.. Το μεγάλο μας καμάρι , το μεγάλο μας στήριγμα , είναι η Γλώσσα μας. Αν το χάσουμε, χαθήκαμε. Να διαβάζουμε όσο μπορούμε.
...μνημονεύετε Διονύσιο Σολωμό και μνημονεύετε Αλέξανδρο Παπαδιαμάντη. Πράγματι είναι η λαλιά που δεν ξέρει από ψέμα. Σαν τα Μαθηματικά ένα πράμα..
Ακριβώς και εγώ την ίδια ερώτηση έκανα σε έναν μαθητή μου που είχαμε δουλέψει ασκήσεις του κυρίου Ζανταριδη από το γνωστό βιβλίο 4 θέμα.
Και πήρα την ίδια απάντηση. Έχασε την αιτιολογηση στο Δ4 γιατι προσπαθούσε με άλλον τρόπο να βγάλει τα πρόσημα με τα ολοκληρώματα και έχασε την ψυχραιμία του.
Μάριος
''Διάλεγε πάντα τον καλλίτερο δρόμο,όσο κι αν δύσκολος μοιάζει, η συνήθεια γρήγορα θα τον κάνει εύκολο κι ευχάριστο'' - Πυθαγόρας.
"Anyone who has never made a mistake has never tried anything new." - Albert Einstein.
''Διάλεγε πάντα τον καλλίτερο δρόμο,όσο κι αν δύσκολος μοιάζει, η συνήθεια γρήγορα θα τον κάνει εύκολο κι ευχάριστο'' - Πυθαγόρας.
"Anyone who has never made a mistake has never tried anything new." - Albert Einstein.
- S.E.Louridas
- Δημοσιεύσεις: 5954
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2015
Επιτρέψτε μου να πω ότι θα ήταν ευχής έργο να ήταν θεματοδότης ... ο Νίκος Ζανταρίδης...
Προσωπικά πιστεύω ότι τα θέματα δεν είχαν Μαθηματικά λάθη. Αλλά αλλοίμονο αν συζητούσαμε σε αυτό το περιβάλλον για εισαγωγικές εξετάσεις. Όμως τι και αν είναι πιο δύσκολα ή πιο εύκολα από προηγούμενες φορές; Σημασία έχει ότι είναι της ίδιας νοοτροπίας με όλα σχεδόν τα θέματα των τελευταίων ετών και επομένως τουλάχιστον από τους profetionals είναι προβλέψιμης νοοτροπίας. Για παράδειγμα γιατί το τελευταίο θέμα πρέπει ντε και καλά να είναι με συνάρτηση με τύπο ολοκλήρωμα; Όμως υπάρχει και το εξής επίσης ερώτημα: Γιατί το σημείο συσσώρευσης της βαθμολογίας για επιτυχία να είναι το 100; Τι να σημαίνει άραγε σωστό θέμα; Κατά την άποψη μου σωστό θέμα σημαίνει 1ο να έχει διακυμαινόμενη στόχευση, να έχει στόχο, 2ο να έχει σημεία που να μπορεί ο λύτης να βάλει την προσωπική του σφραγίδα, 3ο να λειτουργούν οι ειδικές μορφές των εννοιών που εμπλέκονται για να οδηγηθούμε στην λύση και όχι να μην παίζει ρόλο για την λύση η μορφή ας πούμε του τύπου μίας συνάρτησης και 4ο καλό θα είναι να μην κατασκευάζουμε θέματα με την μέθοδο, κατασκευάζω ένα θέμα με την άνεση της άλγεβρας αλλά το ζητώ προς λύση σε επίπεδο πρακτικής αριθμητικής.
Τώρα για το ηθικό δηλαδή το πιο σημαντικό μέρος της υπόθεσης είναι χρέος της πολιτείας μέσω της σωστής παιδείας να διαπλάσει νέους απαλλαγμένους από έναν ιδιότυπο ρατσισμό που οδηγεί στο αποκλειστικό δίπολο επιτυχία ή αποτυχία με όλες της συνέπειες της αποτυχίας αλλά και χωρίς την ικανοποίηση της διαδρομής προς τον στόχο έστω και αν αυτός δεν επιτυγχάνεται εύκολα. Αυτή την διαχρονική διαπαιδαγώγηση θέλουν οι νέοι και όχι το στιγμιαίο πατ-πατ στην πλάτη όταν το παιδί συνδέει την αποτυχία στις εξετάσεις με την προσωπική του αποτυχία ολοκληρωτικά προσφέροντας του ταυτόχρονα επίσης στιγμιαία και κάποιες...αφ' υψηλού λέξεις του πεπειραμένου. Προσωπικά δεν θεωρώ πέσιμο στην ζωή αν δεν πετύχω σε κάποιες εξετάσεις. Αρκεί να διαχειριστώ την αποτυχία σωστά με το να την αγαπήσω ώστε η ίδια να μου πει το μυστικό της για να την ξεπεράσω πετυχαίνοντας. Όμως αυτό θέλει πλάσιμο από την πολιτεία και την παιδεία της από τους γονείς και τους παράγοντες και όλα αυτά με την δύναμη του παραδείγματος από ημάς ή και υμάς. Τέλος θα πρέπει να αποδεχθούμε ως κοινωνία την αριστεία και την αξιοκρατία παντού (στα γράμματα, στη τέχνη, στο εμπόριο κ.τ.λ.) σαν αποτέλεσμα του αντίστοιχου χαρίσματος που ο καθένας από εμάς έχει.
Προσωπικά πιστεύω ότι τα θέματα δεν είχαν Μαθηματικά λάθη. Αλλά αλλοίμονο αν συζητούσαμε σε αυτό το περιβάλλον για εισαγωγικές εξετάσεις. Όμως τι και αν είναι πιο δύσκολα ή πιο εύκολα από προηγούμενες φορές; Σημασία έχει ότι είναι της ίδιας νοοτροπίας με όλα σχεδόν τα θέματα των τελευταίων ετών και επομένως τουλάχιστον από τους profetionals είναι προβλέψιμης νοοτροπίας. Για παράδειγμα γιατί το τελευταίο θέμα πρέπει ντε και καλά να είναι με συνάρτηση με τύπο ολοκλήρωμα; Όμως υπάρχει και το εξής επίσης ερώτημα: Γιατί το σημείο συσσώρευσης της βαθμολογίας για επιτυχία να είναι το 100; Τι να σημαίνει άραγε σωστό θέμα; Κατά την άποψη μου σωστό θέμα σημαίνει 1ο να έχει διακυμαινόμενη στόχευση, να έχει στόχο, 2ο να έχει σημεία που να μπορεί ο λύτης να βάλει την προσωπική του σφραγίδα, 3ο να λειτουργούν οι ειδικές μορφές των εννοιών που εμπλέκονται για να οδηγηθούμε στην λύση και όχι να μην παίζει ρόλο για την λύση η μορφή ας πούμε του τύπου μίας συνάρτησης και 4ο καλό θα είναι να μην κατασκευάζουμε θέματα με την μέθοδο, κατασκευάζω ένα θέμα με την άνεση της άλγεβρας αλλά το ζητώ προς λύση σε επίπεδο πρακτικής αριθμητικής.
Τώρα για το ηθικό δηλαδή το πιο σημαντικό μέρος της υπόθεσης είναι χρέος της πολιτείας μέσω της σωστής παιδείας να διαπλάσει νέους απαλλαγμένους από έναν ιδιότυπο ρατσισμό που οδηγεί στο αποκλειστικό δίπολο επιτυχία ή αποτυχία με όλες της συνέπειες της αποτυχίας αλλά και χωρίς την ικανοποίηση της διαδρομής προς τον στόχο έστω και αν αυτός δεν επιτυγχάνεται εύκολα. Αυτή την διαχρονική διαπαιδαγώγηση θέλουν οι νέοι και όχι το στιγμιαίο πατ-πατ στην πλάτη όταν το παιδί συνδέει την αποτυχία στις εξετάσεις με την προσωπική του αποτυχία ολοκληρωτικά προσφέροντας του ταυτόχρονα επίσης στιγμιαία και κάποιες...αφ' υψηλού λέξεις του πεπειραμένου. Προσωπικά δεν θεωρώ πέσιμο στην ζωή αν δεν πετύχω σε κάποιες εξετάσεις. Αρκεί να διαχειριστώ την αποτυχία σωστά με το να την αγαπήσω ώστε η ίδια να μου πει το μυστικό της για να την ξεπεράσω πετυχαίνοντας. Όμως αυτό θέλει πλάσιμο από την πολιτεία και την παιδεία της από τους γονείς και τους παράγοντες και όλα αυτά με την δύναμη του παραδείγματος από ημάς ή και υμάς. Τέλος θα πρέπει να αποδεχθούμε ως κοινωνία την αριστεία και την αξιοκρατία παντού (στα γράμματα, στη τέχνη, στο εμπόριο κ.τ.λ.) σαν αποτέλεσμα του αντίστοιχου χαρίσματος που ο καθένας από εμάς έχει.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
-
Θεοδωρος Παγωνης
- Δημοσιεύσεις: 311
- Εγγραφή: Τετ Οκτ 26, 2011 2:10 pm
- Τοποθεσία: Αγρίνιο
Re: Μαθηματικά κατεύθυνσης 2015
Μια ακόμη λύση για το Δ3 , από μαθητή , όχι δικό μου , που έτυχε να δω :
Επειδή , από την σχέση
, από την σχέση  , που ισχύει για κάθε
, που ισχύει για κάθε  , θα ισχύουν
, θα ισχύουν
 και
και  .
.
Οπότε για κοντά στο
κοντά στο  με
με  έχω :
έχω :
 (σημείωση δική μου : εδώ «μπάζει» λίγο)
(σημείωση δική μου : εδώ «μπάζει» λίγο)

Όμως ,
,
Από κριτήριο παρεμβολής έχω το ζητούμενο όριο.
Επειδή
 , από την σχέση
, από την σχέση  , που ισχύει για κάθε
, που ισχύει για κάθε  , θα ισχύουν
, θα ισχύουν  και
και  .
.Οπότε για
 κοντά στο
κοντά στο  με
με  έχω :
έχω :  (σημείωση δική μου : εδώ «μπάζει» λίγο)
(σημείωση δική μου : εδώ «μπάζει» λίγο) 
Όμως
 ,
, Από κριτήριο παρεμβολής έχω το ζητούμενο όριο.
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Μαθηματικά κατεύθυνσης 2015
Νίκο, σέβομαι την επιθυμία σου !nick39 έγραψε:Κύριε Στεργίου μιας και αύριο θα ξεκινήσετε τις διορθώσεις θα μπορούσατε μήπως να μας αναφέρετε μερικά στοιχεία το βράδυ; π.χ "διόρθωσα 20 γραπτά...τα 10 ήταν κάτω από τη βάση 7 μέχρι 15 και 3 20αρια???προς φιλοσοφικής συζήτησης και μόνο...
Τονισμός κειμένου
Βέβαια, πρέπει να πω στους φίλους μαθητές και συναδέλφους που μας παρακολουθούν ότι τέτοια στοιχεία δεν έχουν καμία σημασία. Αν δεν έχουμε δείγμα 1000 γραπτών από την ίδια μάλιστα περιοχή με πέρυσι και να έχουμε κρατήσει τα αντίστοιχα στατιστικά , καμία ασφαλής σύγκριση δεν μπορεί να γίνει.
Αυτός είναι ο λόγος που όσοι εμπλεκόμαστε στα Βαθμολογικά κέντρα δεν δίνουμε τέτοια στοιχεία. Με άλλα λόγια δεν τα εμπιστευόμαστε ούτε εμείς οι ίδιοι.
Μην ξεχνάμε επίσης ότι οι εξετάσεις συνεχίζονται και οι μαθητές πρέπει να βλέπουν μπροστά. Φανταστείτε τι θα γίνει αν εμένα μου τύχουν δύο φάκελοι από το Πρύτυπο λύκειο ΧΧΧ και τα 20 γραπτά στα 50 είναι πάνω από 17. Όλοι οι μαθητές που μας βλέπουν θα απογοητευτούν. Οφείλουμε επομένως να υποκλιθούμε στην αγωνία παιδιών και γονιών και να μην κάνουμε επιπόλαιες ανακοινώσεις.
Για αυτόν μόνο το λόγο δεν είναι σωστό κανένας από μας να δώσει τέτοια στοιχεία δημόσια . Σεβόμαστε την επιθυμία των εκλεκτών φίλων και συναδέλφων αλλά και των μαθητών να ακούσουν κάτι από ...πρώτο χέρι, αλλά αυτό πιο πολλά προβλήματα θα επιφέρει παρά θα λύσει . Ας τελειώσουν πρώτα οι εξετάσεις με το καλό , να βρουν τα παιδιά το ρυθμό τους, να έχουμε διορθώσει πάνω από 1000 γραπτά και μετά, πάντα με διακριτικότητα, μπορούμε να κάνουμε κάποια εκτίμηση.
Καλά αποτελέσματα στους μαθητές σας καθώς και στους ίδιους τους μαθητές-μέλη της οικογένειας του mathematica !
Μπάμπης
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Μαθηματικά κατεύθυνσης 2015
Εκτός από το πρόβλημα του Νίκου, αν εκτιμήσει η επιτροπή ότι ο χρόνος είναι υπεραρκετός , όπως συνηθίζεται άλλωστε για χρόνια , πρέπει να συμπληρωθεί από την επιτροπή και το εξής ερώτημα (με κατάλληλη συρραφή βέβαια) :nikoszan έγραψε:Μια άσκηση(ιδέα για μελλοντικης μορφής θέμα?) αφιερωμένη στους φίλους θεματοδότες ,που τόσο πολύ έχουν κατακριθεί.(ΧΡΟΝΟΣ ΛΥΣΗΣ 15min με σχολικά μαθηματικά και με πλήρη διατύπωση)
Έστω η τρεις φορές παραγωγίσιμη συνάρτηση,για την οποία ισχύει :
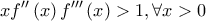
και το σημείοβρίσκεται κάτω απο το μέσο του ευθ. τμήματος
,όπου
και
.
Να βρεθεί το όριο :.
Ερώτηση 1 : Είναι επαρκής ο χρόνος ?
Ερώτηση 2 :Έχουν διδαχθεί οι μαθητές και όχι μόνο τέτοιας μορφής θέμα.
Ερώτηση 3:Μήπως είμαι αρκετά κακός θεματοδότης(ισχυρίζομαι οτι δεν έχω τέτοια πρόθεση)
ΣΧΟΛΙΟ1:Για να μην παρεξηγηθώ , τα θέματα απο μαθηματικη άποψη είναι άψογα και ειναι σχεδόν ταυτόσημα της νοοτροπίας με την οποία προπονώ τους μαθητές.
Θα σχολιάσω όμως μόνο ένα(υπάρχουν και άλλα ) : ότι ο χρόνος των τριών ωρών δεν έφτανε να απαντηθούν με πλήρη διατύπωση τα θέματα αυτά απο τους
περισσότερους μαθητές και οχι μόνο (ΠΡΟΤΕΙΝΟΜΕΝΟΣ ΧΡΟΝΟΣ:(ΧΡΟΝΟΣ ΚΑΘΗΓΗΤΗ ΛΥΤΗ ΜΕ ΠΛΗΡΗ ΔΙΑΤΥΠΩΣΗ )Χ3)
ΣΧΟΛΙΟ2Αν ο χρονος των 15min δεν φτάνει ,για να απαντηθεί το προτεινόμενο θέμα, δινεται επι πλεον χρόνος 5 min.
ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ: ΟΤΑΝ ΠΕΦΤΟΥΜΕ ΠΡΕΠΕΙ ΝΑ ΒΡΟΥΜΕ ΤΗΝ ΔΥΝΑΜΗ ΝΑ ΣΗΚΩΘΟΥΜΕ! ΚΑΛΗ ΕΠΙΤΥΧΙΑ!!
Ν.Ζ.
ΑΣΚΗΣΗ
Δίνεται συνεχής συνάρτηση
 στο
στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) και η παράσταση
και η παράσταση  .
.α) Να βρείτε τη μέγιστη τιμή της παράστασης
 .
.β) Αν η παράσταση
 είναι ελάχιστη, να βρείτε τον τύπο της
είναι ελάχιστη, να βρείτε τον τύπο της  .
.Υπόδειξη(για να μην ασχολείστε με τόσο τετριμμένες ασκήσεις
Και δεν θα είναι λίγοι εκείνοι που θα βαράνε παλαμάκια ότι η επιτροπή πρωτοτύπισε ! Μόλις θα δούνε τη λύση ( που θα κάνουν οι άλλοι, όχι οι ίδιοι! )θα σου πούνε, '' χωρίς να ξέρεις να συμπληρώνεις τετράγωνο , που πας ...ρε Καραμήτρο !'' ;
Όπως διαβλέπω, ειδικά με την μείωση των μαθημάτων και με την απόφαση να ρίξουμε όσο πιο χαμηλά τις βάσεις, από του χρόνου μόνο με τέτοια ερωτήματα
θα πρέπει να ασχολούμαστε για να πιάσει κάποιος το άριστα και για να νοιώθουμε ότι κάτι κάναμε.
Μπάμπης
τελευταία επεξεργασία από Μπάμπης Στεργίου σε Τετ Μάιος 27, 2015 11:06 am, έχει επεξεργασθεί 1 φορά συνολικά.
-
mathfinder
- Διευθύνον Μέλος
- Δημοσιεύσεις: 519
- Εγγραφή: Πέμ Ιαν 01, 2009 11:56 pm
Re: Μαθηματικά κατεύθυνσης 2015
Στο Γ4 μπορούμε να δείξουμε ότι η  είναι συνεχής στο
είναι συνεχής στο  χρησιμοποιώντας τη σχέση από το Γ3 :
χρησιμοποιώντας τη σχέση από το Γ3 :  και συνεχίζουμε με κριτήριο παρεμβολής.
και συνεχίζουμε με κριτήριο παρεμβολής.
Αθ. Μπεληγιάννης
 είναι συνεχής στο
είναι συνεχής στο  χρησιμοποιώντας τη σχέση από το Γ3 :
χρησιμοποιώντας τη σχέση από το Γ3 :  και συνεχίζουμε με κριτήριο παρεμβολής.
και συνεχίζουμε με κριτήριο παρεμβολής.Αθ. Μπεληγιάννης
Never stop learning , because life never stops teaching.
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Μαθηματικά κατεύθυνσης 2015
Θανάση, όταν υπάρχει ηρεμία , βλέπουμε υπέροχα πράγματα !mathfinder έγραψε:Στο Γ4 μπορούμε να δείξουμε ότι ηείναι συνεχής στο
χρησιμοποιώντας τη σχέση από το Γ3 :
και συνεχίζουμε με κριτήριο παρεμβολής.
Αθ. Μπεληγιάννης
Καλές διορθώσεις !!!
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2015
Στο Δ1 αφότου φτάσουμε στη σχέση 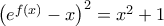 , για κάθε
, για κάθε  μπορούμε να εξάγουμε τον τύπο της
μπορούμε να εξάγουμε τον τύπο της  με τον εξής τρόπο (χωρίς μάλιστα να απαιτείται να χρησιμοποιήσουμε τη συνέχεια της συνάρτησης
με τον εξής τρόπο (χωρίς μάλιστα να απαιτείται να χρησιμοποιήσουμε τη συνέχεια της συνάρτησης  λόγω της ειδικής περίπτωσης που έχουμε):
λόγω της ειδικής περίπτωσης που έχουμε):
Αν υπήρχε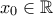 ώστε
ώστε  τότε επειδή το 1ο μέλος είναι θετικό, οφείλει και το 2ο μέλος να είναι θετικό.
τότε επειδή το 1ο μέλος είναι θετικό, οφείλει και το 2ο μέλος να είναι θετικό.
Όμως , άτοπο.
, άτοπο.
Συνεπώς , για κάθε
, για κάθε  .
.
Εναλλακτικά για το Δ1, αφού φτάσουμε στη σχέση , για κάθε
, για κάθε  μπορούμε να δούμε την τελευταία παράσταση ως τριώνυμο του
μπορούμε να δούμε την τελευταία παράσταση ως τριώνυμο του  με διακρίνουσα
με διακρίνουσα 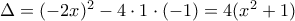
Άρα έχουμε , για κάθε
, για κάθε 
Τώρα συνεχίζουμε όπως παραπάνω για να απορρίψουμε τη δεύτερη περίπτωση: "Αν υπήρχε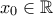 ώστε
ώστε  τότε ... "
τότε ... "
Αλέξανδρος
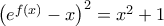 , για κάθε
, για κάθε  μπορούμε να εξάγουμε τον τύπο της
μπορούμε να εξάγουμε τον τύπο της  με τον εξής τρόπο (χωρίς μάλιστα να απαιτείται να χρησιμοποιήσουμε τη συνέχεια της συνάρτησης
με τον εξής τρόπο (χωρίς μάλιστα να απαιτείται να χρησιμοποιήσουμε τη συνέχεια της συνάρτησης  λόγω της ειδικής περίπτωσης που έχουμε):
λόγω της ειδικής περίπτωσης που έχουμε):Αν υπήρχε
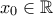 ώστε
ώστε  τότε επειδή το 1ο μέλος είναι θετικό, οφείλει και το 2ο μέλος να είναι θετικό.
τότε επειδή το 1ο μέλος είναι θετικό, οφείλει και το 2ο μέλος να είναι θετικό. Όμως
 , άτοπο.
, άτοπο.Συνεπώς
 , για κάθε
, για κάθε  .
.Εναλλακτικά για το Δ1, αφού φτάσουμε στη σχέση
 , για κάθε
, για κάθε  μπορούμε να δούμε την τελευταία παράσταση ως τριώνυμο του
μπορούμε να δούμε την τελευταία παράσταση ως τριώνυμο του  με διακρίνουσα
με διακρίνουσα 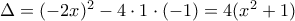
Άρα έχουμε
 , για κάθε
, για κάθε 
Τώρα συνεχίζουμε όπως παραπάνω για να απορρίψουμε τη δεύτερη περίπτωση: "Αν υπήρχε
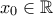 ώστε
ώστε  τότε ... "
τότε ... "Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Θεοδωρος Παγωνης
- Δημοσιεύσεις: 311
- Εγγραφή: Τετ Οκτ 26, 2011 2:10 pm
- Τοποθεσία: Αγρίνιο
Re: Μαθηματικά κατεύθυνσης 2015
Καλησπέρα Αλέξανδρε :
Η δεύτερη περίπτωση μπορεί να απορριφθεί πιο εύκολα με την αρχική συνθήκη για την , δηλαδή με το
, δηλαδή με το  .
.
Πράγματι , η δεύτερη περίπτωση για γίνεται
γίνεται
 , άτοπο .
, άτοπο .
Η δεύτερη περίπτωση μπορεί να απορριφθεί πιο εύκολα με την αρχική συνθήκη για την
 , δηλαδή με το
, δηλαδή με το  .
.Πράγματι , η δεύτερη περίπτωση για
 γίνεται
γίνεται  , άτοπο .
, άτοπο .Re: Μαθηματικά κατεύθυνσης 2015
Το παραπάνω δεν αποτελεί πλήρη απόδειξη ότι η δεύτερη περίπτωση δεν ισχύει.Θεοδωρος Παγωνης έγραψε:Καλησπέρα Αλέξανδρε :
Η δεύτερη περίπτωση μπορεί να απορριφθεί πιο εύκολα με την αρχική συνθήκη για την, δηλαδή με το
.
Πράγματι , η δεύτερη περίπτωση γιαγίνεται
, άτοπο .
Η συνάρτηση μπορεί να έχει τον ένα τύπο για κάποια
 και τον άλλο τύπο για κάποια άλλα.
και τον άλλο τύπο για κάποια άλλα.Το παραπάνω απλά επιβεβαιώνει ότι για
 η
η  έχει τον τύπο
έχει τον τύπο  .
.Γιώργος Γαβριλόπουλος
Re: Μαθηματικά κατεύθυνσης 2015
Αλέξαντρε, ναί!!cretanman έγραψε:Στο Δ1 αφότου φτάσουμε στη σχέση, για κάθε
μπορούμε να εξάγουμε τον τύπο της
με τον εξής τρόπο (χωρίς τη συνέχεια της συνάρτησης
λόγω της ειδικής περίπτωσης που έχουμε):
Αν υπήρχεώστε
τότε επειδή το 1ο μέλος είναι θετικό, οφείλει και το 2ο μέλος να είναι θετικό.
Όμως, άτοπο.
Συνεπώς, για κάθε
.
Αυτή η παρατήρηση αξίζει ...
Νῆφε καί μέμνασο ἀπιστεῖν˙ ἄρθρα ταῦτα γάρ φρενῶν
Νοῦς ὁρᾷ καί Νοῦς ἀκούει˙ τἆλλα κωφά καί τυφλά.
...
Νοῦς ὁρᾷ καί Νοῦς ἀκούει˙ τἆλλα κωφά καί τυφλά.
...
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2015
Δυστυχώς, δεν ισχύει η παραπάνω σχέση...Θεοδωρος Παγωνης έγραψε:Μια ακόμη λύση για το Δ3 , από μαθητή , όχι δικό μου , που έτυχε να δω :
Επειδή, από την σχέση
, που ισχύει για κάθε
, θα ισχύουν
και
.
Οπότε γιακοντά στο
με
έχω :
(σημείωση δική μου : εδώ «μπάζει» λίγο)
Όμως,
Από κριτήριο παρεμβολής έχω το ζητούμενο όριο.
Θανάσης Κοντογεώργης
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2015
nikoszan έγραψε:Μια άσκηση(ιδέα για μελλοντικης μορφής θέμα?) αφιερωμένη στους φίλους θεματοδότες ,που τόσο πολύ έχουν κατακριθεί.(ΧΡΟΝΟΣ ΛΥΣΗΣ 15min με σχολικά μαθηματικά και με πλήρη διατύπωση)
Έστω η τρεις φορές παραγωγίσιμη συνάρτηση,για την οποία ισχύει :
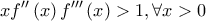
και το σημείοβρίσκεται κάτω απο το μέσο του ευθ. τμήματος
,όπου
και
.
Να βρεθεί το όριο :.
Ερώτηση 1 : Είναι επαρκής ο χρόνος ?
Ερώτηση 2 :Έχουν διδαχθεί οι μαθητές και όχι μόνο τέτοιας μορφής θέμα.
Ερώτηση 3:Μήπως είμαι αρκετά κακός θεματοδότης(ισχυρίζομαι οτι δεν έχω τέτοια πρόθεση)
ΣΧΟΛΙΟ1:Για να μην παρεξηγηθώ , τα θέματα απο μαθηματικη άποψη είναι άψογα και ειναι σχεδόν ταυτόσημα της νοοτροπίας με την οποία προπονώ τους μαθητές.
Θα σχολιάσω όμως μόνο ένα(υπάρχουν και άλλα ) : ότι ο χρόνος των τριών ωρών δεν έφτανε να απαντηθούν με πλήρη διατύπωση τα θέματα αυτά απο τους
περισσότερους μαθητές και οχι μόνο (ΠΡΟΤΕΙΝΟΜΕΝΟΣ ΧΡΟΝΟΣ:(ΧΡΟΝΟΣ ΚΑΘΗΓΗΤΗ ΛΥΤΗ ΜΕ ΠΛΗΡΗ ΔΙΑΤΥΠΩΣΗ )Χ3)
ΣΧΟΛΙΟ2Αν ο χρονος των 15min δεν φτάνει ,για να απαντηθεί το προτεινόμενο θέμα, δινεται επι πλεον χρόνος 5 min.
ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ: ΟΤΑΝ ΠΕΦΤΟΥΜΕ ΠΡΕΠΕΙ ΝΑ ΒΡΟΥΜΕ ΤΗΝ ΔΥΝΑΜΗ ΝΑ ΣΗΚΩΘΟΥΜΕ! ΚΑΛΗ ΕΠΙΤΥΧΙΑ!!
Ν.Ζ.
Δείτε και εδώ:
viewtopic.php?f=55&t=49712
Θανάσης Κοντογεώργης
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2015
Grosrouvre έγραψε:Φυσικά, ως ώφειλε,.
Μπορούμε να δείξουμε, χωρίς τη χρήση υπολογιστή ότι,

viewtopic.php?f=61&t=49753
Θανάσης Κοντογεώργης
-
tolis riza
- Δημοσιεύσεις: 65
- Εγγραφή: Παρ Ιουν 17, 2011 9:38 pm
Re: Μαθηματικά κατεύθυνσης 2015
Μια εναλλακτική λύση στο ερώτημα Γ3
Η δοθείσα σχέση γράφεται
 (1).
(1).
Το πρώτο μέλος της (1) εκφράζει το εμβαδόν του χωρίου Χ που ορίζεται από τις ευθείες και
και  , την
, την  και τον άξονα t΄t . Το δεύτερο μέλος εκφράζει το εμβαδόν του ορθογωνίου που σχηματίζεται από τις ευθείες
και τον άξονα t΄t . Το δεύτερο μέλος εκφράζει το εμβαδόν του ορθογωνίου που σχηματίζεται από τις ευθείες  ,
,  , τον άξονα t΄t και την ευθεία
, τον άξονα t΄t και την ευθεία  . Εφόσον η
. Εφόσον η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\displaystyle [2x,4x] \displaystyle [2x,4x]](/forum/ext/geomar/texintegr/latexrender/pictures/dc43cf6aa6eed66c538048e8ae1cf00c.png) , το
, το  είναι η μέγιστη τιμή της στο
είναι η μέγιστη τιμή της στο ![\displaystyle [2x,4x] \displaystyle [2x,4x]](/forum/ext/geomar/texintegr/latexrender/pictures/dc43cf6aa6eed66c538048e8ae1cf00c.png) . Άρα όλα τα σημεία της
. Άρα όλα τα σημεία της  (εκτός από το σημείο τομής τής
(εκτός από το σημείο τομής τής  με την ευθεία
με την ευθεία  ) βρίσκονται κάτω από την ευθεία
) βρίσκονται κάτω από την ευθεία  . Αυτό σημαίνει ότι το ορθογώνιο περιέχει το χωρίο Χ και άρα η (1) ισχύει.
. Αυτό σημαίνει ότι το ορθογώνιο περιέχει το χωρίο Χ και άρα η (1) ισχύει.
Αριστείδης Μουζακίτης
Η δοθείσα σχέση γράφεται
 (1).
(1). Το πρώτο μέλος της (1) εκφράζει το εμβαδόν του χωρίου Χ που ορίζεται από τις ευθείες
 και
και  , την
, την  και τον άξονα t΄t . Το δεύτερο μέλος εκφράζει το εμβαδόν του ορθογωνίου που σχηματίζεται από τις ευθείες
και τον άξονα t΄t . Το δεύτερο μέλος εκφράζει το εμβαδόν του ορθογωνίου που σχηματίζεται από τις ευθείες  ,
,  , τον άξονα t΄t και την ευθεία
, τον άξονα t΄t και την ευθεία  . Εφόσον η
. Εφόσον η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\displaystyle [2x,4x] \displaystyle [2x,4x]](/forum/ext/geomar/texintegr/latexrender/pictures/dc43cf6aa6eed66c538048e8ae1cf00c.png) , το
, το  είναι η μέγιστη τιμή της στο
είναι η μέγιστη τιμή της στο ![\displaystyle [2x,4x] \displaystyle [2x,4x]](/forum/ext/geomar/texintegr/latexrender/pictures/dc43cf6aa6eed66c538048e8ae1cf00c.png) . Άρα όλα τα σημεία της
. Άρα όλα τα σημεία της  (εκτός από το σημείο τομής τής
(εκτός από το σημείο τομής τής  με την ευθεία
με την ευθεία  ) βρίσκονται κάτω από την ευθεία
) βρίσκονται κάτω από την ευθεία  . Αυτό σημαίνει ότι το ορθογώνιο περιέχει το χωρίο Χ και άρα η (1) ισχύει.
. Αυτό σημαίνει ότι το ορθογώνιο περιέχει το χωρίο Χ και άρα η (1) ισχύει.Αριστείδης Μουζακίτης
- Συνημμένα
-
- figure1 (2)-001.jpg (27.46 KiB) Προβλήθηκε 3627 φορές
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες

![\displaystyle{\begin{array}{l}
{\Delta _1}\mathop {}\limits_{}^{} :\\
\mathop {}\limits_{}^{} f'(x)\left[ {{e^{f(x)}} + {e^{ - f(x)}}} \right] = 2\mathop {}\limits_{}^{} \Rightarrow \mathop {}\limits_{}^{} \left[ {{e^{f(x)}} + {e^{ - f(x)}}} \right] = \frac{2}{{f'(x)}}\mathop {}\limits_{}^{} \mathop \Rightarrow \limits^{y = f(x)} \mathop {}\limits_{}^{} \\
\left[ {{e^y} + {e^{ - y}}} \right] = 2\frac{{d{f^{ - 1}}(y)}}{{dy}}\mathop {}\limits_{}^{} \Rightarrow \mathop {}\limits_{}^{} {f^{ - 1}}(y) = \frac{1}{2}\left[ {{e^y} + {e^{ - y}}} \right]\mathop {}\limits_{}^{} \Rightarrow \mathop {}\limits_{}^{} f(x) = \ln \left( {x + \sqrt {{x^2} + 1} } \right)\\
\\
{\Delta _2}\mathop {}\limits_{}^{} :\mathop {}\limits_{}^{} \\
E = \frac{1}{2} - \int_0^{\ln \left( {1 + \sqrt 2 } \right)} {\left[ {\ln \left( {1 + \sqrt 2 } \right) - {f^{ - 1}}(x)} \right]} dx = \\
\\
\frac{1}{2} - \ln \left( {1 + \sqrt 2 } \right) + \int_0^{\ln \left( {1 + \sqrt 2 } \right)} {{f^{ - 1}}(x)dx} \mathop {}\limits_{}^{} = \mathop {}\limits_{}^{} \frac{1}{2} - \ln \left( {1 + \sqrt 2 } \right) + \frac{1}{2}\int_0^{\ln \left( {1 + \sqrt 2 } \right)} {\left( {{e^x} - {e^{ - x}}} \right)dx} = \\
= \sqrt 2 - \frac{1}{2} - \ln \left( {1 + \sqrt 2 } \right)
\end{array}} \displaystyle{\begin{array}{l}
{\Delta _1}\mathop {}\limits_{}^{} :\\
\mathop {}\limits_{}^{} f'(x)\left[ {{e^{f(x)}} + {e^{ - f(x)}}} \right] = 2\mathop {}\limits_{}^{} \Rightarrow \mathop {}\limits_{}^{} \left[ {{e^{f(x)}} + {e^{ - f(x)}}} \right] = \frac{2}{{f'(x)}}\mathop {}\limits_{}^{} \mathop \Rightarrow \limits^{y = f(x)} \mathop {}\limits_{}^{} \\
\left[ {{e^y} + {e^{ - y}}} \right] = 2\frac{{d{f^{ - 1}}(y)}}{{dy}}\mathop {}\limits_{}^{} \Rightarrow \mathop {}\limits_{}^{} {f^{ - 1}}(y) = \frac{1}{2}\left[ {{e^y} + {e^{ - y}}} \right]\mathop {}\limits_{}^{} \Rightarrow \mathop {}\limits_{}^{} f(x) = \ln \left( {x + \sqrt {{x^2} + 1} } \right)\\
\\
{\Delta _2}\mathop {}\limits_{}^{} :\mathop {}\limits_{}^{} \\
E = \frac{1}{2} - \int_0^{\ln \left( {1 + \sqrt 2 } \right)} {\left[ {\ln \left( {1 + \sqrt 2 } \right) - {f^{ - 1}}(x)} \right]} dx = \\
\\
\frac{1}{2} - \ln \left( {1 + \sqrt 2 } \right) + \int_0^{\ln \left( {1 + \sqrt 2 } \right)} {{f^{ - 1}}(x)dx} \mathop {}\limits_{}^{} = \mathop {}\limits_{}^{} \frac{1}{2} - \ln \left( {1 + \sqrt 2 } \right) + \frac{1}{2}\int_0^{\ln \left( {1 + \sqrt 2 } \right)} {\left( {{e^x} - {e^{ - x}}} \right)dx} = \\
= \sqrt 2 - \frac{1}{2} - \ln \left( {1 + \sqrt 2 } \right)
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/ce327ec4c93d5fcae1aa813d17798114.png)