Οι εσωτερικές διχοτόμοι τριγώνου
 τέμνουν τις απέναντι πλευρές στα σημεία
τέμνουν τις απέναντι πλευρές στα σημεία 
Αποδείξτε ότι ικανή και αναγκαία συνθήκη για να είναι το τρίγωνο
 ισόπλευρο είναι
ισόπλευρο είναι 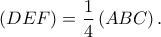
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
 τέμνουν τις απέναντι πλευρές στα σημεία
τέμνουν τις απέναντι πλευρές στα σημεία 
 ισόπλευρο είναι
ισόπλευρο είναι 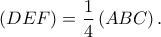

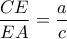 και
και 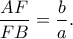
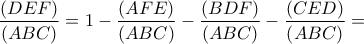







 του τριγώνου
του τριγώνου  ισχύει
ισχύει 
 είναι τα μέσα των πλευρών
είναι τα μέσα των πλευρών  αντίστοιχα του τριγώνου
αντίστοιχα του τριγώνου  (Η απόδειξη είναι όμοια με την παραπάνω και σίγουρα έχει ξανασυζητηθεί στο
(Η απόδειξη είναι όμοια με την παραπάνω και σίγουρα έχει ξανασυζητηθεί στο Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες