 ας είναι
ας είναι  τα σημεία τομής κύκλου εφαπτόμενου των
τα σημεία τομής κύκλου εφαπτόμενου των  με την
με την  και ας είναι
και ας είναι  πλησιέστερα του
πλησιέστερα του  .
.Να δειχθεί ότι
 , όπου
, όπου  τα σημεία τομής του έγκυκλου του
τα σημεία τομής του έγκυκλου του  με τις
με τις  αντίστοιχα, με
αντίστοιχα, με  πλησιέστερα του
πλησιέστερα του  και
και  πλησιέστερα του
πλησιέστερα του  .
.Στάθης
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
 ας είναι
ας είναι  τα σημεία τομής κύκλου εφαπτόμενου των
τα σημεία τομής κύκλου εφαπτόμενου των  με την
με την  και ας είναι
και ας είναι  πλησιέστερα του
πλησιέστερα του  .
. , όπου
, όπου  τα σημεία τομής του έγκυκλου του
τα σημεία τομής του έγκυκλου του  με τις
με τις  αντίστοιχα, με
αντίστοιχα, με  πλησιέστερα του
πλησιέστερα του  και
και  πλησιέστερα του
πλησιέστερα του  .
.Καλησπέρα,ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε:Σε ισοσκελές τραπέζιοας είναι
τα σημεία τομής κύκλου εφαπτόμενου των
με την
και ας είναι
πλησιέστερα του
.
Να δειχθεί ότι, όπου
τα σημεία τομής του έγκυκλου του
με τις
αντίστοιχα, με
πλησιέστερα του
και
πλησιέστερα του
.
Στάθης
 ο κύκλος που εφάπτεται της
ο κύκλος που εφάπτεται της  και διέρχεται από τα σημεία
και διέρχεται από τα σημεία  και
και  ο κύκλος που εφάπτεται της
ο κύκλος που εφάπτεται της  και διέρχεται από τα σημεία
και διέρχεται από τα σημεία  .
. , του κύκλου
, του κύκλου  με την
με την  σύμφωνα με την παραπάνω κατασκευή, προσδιορίζεται ως εξής:
σύμφωνα με την παραπάνω κατασκευή, προσδιορίζεται ως εξής:  . Κατασκευάζουμε ημικύκλιο διαμέτρου
. Κατασκευάζουμε ημικύκλιο διαμέτρου  και φέρουμε την κάθετο προς την διάμετρο στο σημείο
και φέρουμε την κάθετο προς την διάμετρο στο σημείο  . Έστω
. Έστω  το σημείο τομής αυτής με την διάμετρο. Τότε το σημείο επαφής
το σημείο τομής αυτής με την διάμετρο. Τότε το σημείο επαφής  βρίσκεται σε απόσταση από το
βρίσκεται σε απόσταση από το  ίση με
ίση με 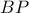 .
. . Αν
. Αν  το σημείο επαφής του με την
το σημείο επαφής του με την  τότε
τότε  . Όπου
. Όπου  το σημείο τομής του ημικυκλίου διαμέτρου
το σημείο τομής του ημικυκλίου διαμέτρου  με την κάθετο από το σημείο
με την κάθετο από το σημείο  .
. οπότε έχουμε
οπότε έχουμε 
 (1)
(1) το σημείο επαφής με την
το σημείο επαφής με την  του εφαπτόμενου κύκλου στις ευθείες
του εφαπτόμενου κύκλου στις ευθείες  και έστω
και έστω  το σημείο επαφής αυτού με την
το σημείο επαφής αυτού με την  .
.
 (2)
(2) (3) και από την (2) έχουμε
(3) και από την (2) έχουμε  (4)
(4) ,
, 
 ,
, 

 ( τα
( τα  τα σημεία επαφής του εφαπτόμενου κύκλου στις ευθείες
τα σημεία επαφής του εφαπτόμενου κύκλου στις ευθείες  ). Άρα
). Άρα  .
. ταυτίζονται αν ισχύει
ταυτίζονται αν ισχύει  . Έστω ότι δεν ταυτίζονται. Τα κέντρα τους θα βρίσκονται επί της μεσοκαθέτου της
. Έστω ότι δεν ταυτίζονται. Τα κέντρα τους θα βρίσκονται επί της μεσοκαθέτου της  , που είναι κοινή χορδή αυτών. Τότε από την δύναμη σημείου , του
, που είναι κοινή χορδή αυτών. Τότε από την δύναμη σημείου , του  , προς αυτούς τους κύκλους έχουμε
, προς αυτούς τους κύκλους έχουμε  (5)
(5) (6)
(6)
 και
και  έχουμε
έχουμε  , όπου
, όπου  το μέσο του τμήματος
το μέσο του τμήματος  και
και  οι προβολές στη μεσοκάθετο του
οι προβολές στη μεσοκάθετο του  των
των  . Δηλαδή τα σημεία
. Δηλαδή τα σημεία  βρίσκονται στην ίδια κάθετη προς την μεσοκάθετο του
βρίσκονται στην ίδια κάθετη προς την μεσοκάθετο του  , πράγμα άτοπο. Άρα τα
, πράγμα άτοπο. Άρα τα  ταυτίζονται και το ίδιο και οι κύκλοι
ταυτίζονται και το ίδιο και οι κύκλοι  .
.  εφάπτεται εσωτερικά της γωνίας
εφάπτεται εσωτερικά της γωνίας  όπως και ο εγγεγραμμένος κύκλος του τριγώνου
όπως και ο εγγεγραμμένος κύκλος του τριγώνου  . Οπότε οι δυο αυτοί κύκλοι είναι ομοιόθετοι με κέντρο ομοιοθεσίας το
. Οπότε οι δυο αυτοί κύκλοι είναι ομοιόθετοι με κέντρο ομοιοθεσίας το  . Λόγο της ομοιθεσίας η χορδή
. Λόγο της ομοιθεσίας η χορδή  θα είναι παράλληλη με την ομόλογη της
θα είναι παράλληλη με την ομόλογη της  . Τα
. Τα  όμως βρίσκονται επί της
όμως βρίσκονται επί της  οπότε
οπότε  .
. Έστω
Έστω  , οι κύκλοι με χορδές τα τμήματα
, οι κύκλοι με χορδές τα τμήματα  αντιστοίχως, όπως ορίζονται στην εκφώνηση και ας είναι
αντιστοίχως, όπως ορίζονται στην εκφώνηση και ας είναι  , ο εγγεγραμμένος κύκλος του τριγώνου
, ο εγγεγραμμένος κύκλος του τριγώνου  , συμμετρικός ( προφανές ) του
, συμμετρικός ( προφανές ) του  ως προς την ευθεία
ως προς την ευθεία  , όπου
, όπου 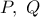 είναι τα μέσα των βάσεων
είναι τα μέσα των βάσεων  αντιστοίχως, του δοσμένου ισοσκελούς τραπεζίου
αντιστοίχως, του δοσμένου ισοσκελούς τραπεζίου  .
. , όπου
, όπου  , με
, με  το κέντρο του κύκλου
το κέντρο του κύκλου  και
και  τον περίκυκλο του
τον περίκυκλο του  και ας είναι
και ας είναι 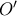 , το συμετρικό σημείο του
, το συμετρικό σημείο του  ως προς το
ως προς το  .
. , με κέντρο το σημείο
, με κέντρο το σημείο 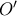 που εφάπτεται των ευθειών
που εφάπτεται των ευθειών  , τέμνει την
, τέμνει την  στα σημεία έστω
στα σημεία έστω  και ας είναι το
και ας είναι το 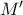 πλησιέστερα στο
πλησιέστερα στο  .
. , τα σημεία τομής των κύκλων
, τα σημεία τομής των κύκλων  και ας είναι
και ας είναι  , τα σημεία τομής των ευθειών
, τα σημεία τομής των ευθειών  αντιστοίχως, από την ευθεία
αντιστοίχως, από την ευθεία  , τα οποία ταυτίζονται με τις προβολές του
, τα οποία ταυτίζονται με τις προβολές του  επί των
επί των  , αντιστοίχως ( γνωστό αποτέλεσμα που αποδεικνύεται εύκολα ).
, αντιστοίχως ( γνωστό αποτέλεσμα που αποδεικνύεται εύκολα ). Από
Από  και
και  έχουμε ότι τα ορθογώνια τρίγωνα
έχουμε ότι τα ορθογώνια τρίγωνα  είναι ίσα και άρα, ισχύει
είναι ίσα και άρα, ισχύει 
 έχουμε
έχουμε  και
και 

 και άρα, το σημείο
και άρα, το σημείο  ανήκει στην ευθεία
ανήκει στην ευθεία  .
.
 Από
Από  , σύμφωνα με το παρακάτω Λήμμα , έχουμε
, σύμφωνα με το παρακάτω Λήμμα , έχουμε  και
και  .
. δηλαδή, είναι συμμετρικά των
δηλαδή, είναι συμμετρικά των  αντιστοίχως, ως προς το μέσον
αντιστοίχως, ως προς το μέσον  του τμήματος
του τμήματος  .
. είναι ομοιόθετοι ως προς το σημείο
είναι ομοιόθετοι ως προς το σημείο  και άρα, ισχύει
και άρα, ισχύει  όπου
όπου  και
και  .
. τώρα, είναι συμμετρικές των
τώρα, είναι συμμετρικές των  αντιστοίχως, ως προς την ευθεία
αντιστοίχως, ως προς την ευθεία  , όπως και οι κύκλοι
, όπως και οι κύκλοι  και επομένως τα τμήματα
και επομένως τα τμήματα  έχουν τα άκρα τους συμμετρικά ως προς την ευθεία
έχουν τα άκρα τους συμμετρικά ως προς την ευθεία  και ανήκουν στην ίδια ευθεία λόγω
και ανήκουν στην ίδια ευθεία λόγω  .
. και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. οι οποίοι τέμνονται στα σημεί έστω
οι οποίοι τέμνονται στα σημεί έστω  και έστω τυχόν σημείο
και έστω τυχόν σημείο  . Η διά του σημείου
. Η διά του σημείου  κάθετη ευθεία επί την
κάθετη ευθεία επί την  , όπου
, όπου  είναι το μέσον της διακέντρου
είναι το μέσον της διακέντρου  των δοσμένων κύκλων
των δοσμένων κύκλων  , τους τέμνει στα ζεύγη των σημείων
, τους τέμνει στα ζεύγη των σημείων  και
και  αντιστοίχως και ας είναι τα
αντιστοίχως και ας είναι τα  εσωτερικά σημεία των
εσωτερικά σημεία των  , αντιστοίχως. Αποδείξτε ότι
, αντιστοίχως. Αποδείξτε ότι  και
και  .
. θερμές ευχές για ειρηνιικό και δημιουργικό το 2016, να έχετε υγεία και κάθε χαρά με τους ανθρώπους που αγαπάτε.
θερμές ευχές για ειρηνιικό και δημιουργικό το 2016, να έχετε υγεία και κάθε χαρά με τους ανθρώπους που αγαπάτε.'Εστωvittasko έγραψε:ΛΗΜΜΑ. - Δίνονται δύο κύκλοιοι οποίοι τέμνονται στα σημεί έστω
και έστω τυχόν σημείο
. Η διά του σημείου
κάθετη ευθεία επί την
, όπου
είναι το μέσον της διακέντρου
των δοσμένων κύκλων
, τους τέμνει στα ζεύγη των σημείων
και
αντιστοίχως και ας είναι τα
εσωτερικά σημεία των
, αντιστοίχως. Αποδείξτε ότι
και
.
 , οι προβολές των κέντρων
, οι προβολές των κέντρων  των δοσμένων κύκλων
των δοσμένων κύκλων  αντιστοίχως και από
αντιστοίχως και από  έχουμε
έχουμε  λόγω
λόγω  .
.
 Από
Από 

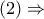








 και
και 

 και
και  και
και 
 και το Λήμμα έχει αποδειχθεί.
και το Λήμμα έχει αποδειχθεί.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες