Για να το δούμε και αυτό που έχει μείνει..(φαίνεται πιο "τρομακτικό" από ότι είναι).

- simsonas.png (84.22 KiB) Προβλήθηκε 1721 φορές
Γενίκευση:Έστω τρίγωνο

και σημείο

του

.Έτσω τυχαίες σεβιανές του τριγώνου που συντρέχουν σε σημείο

.Ορίζουμε

την τομή της

με την εκ του

κάθετη στην

.Ανάλογα ορίζονται και τα

.Έστω

ο ποδικός κύκλος ως προς το

ως προς το

.Τότε το κέντρο του κύκλου αυτού

βρίσκεται στην ευθεία Simson του

ως προς το

(
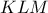
)
Στέλνοντας το

στο άπειρο παίρνουμε το αρχικό.
Για την απόδειξη της γενίκευσης παίρνουμε αντιστροφή κέντρου

:(δε συμβολίζω με τόνους τα αντίστροφα για ευνόητους λόγους...)
Τα

πάνε σε ευθεία.
Οι
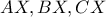
πάνε στους ομοαξονικούς κύκλους
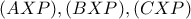
.
Τα

πάνε στα αντιδιαμετρικά των

ως προς τους
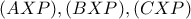
αντίστοιχα.
Επειδή τα

είναι ομοκυκλικά,όπως και τα αντίστοιχά τους,(και λόγω του

κτλ.), το

πάει στην τομή της εκ του

κάθετης στην
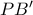
με την εκ του

κάθετη στην
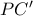
.(Όμοια και για τα άλλα).
Επειδή

κτλ. το

πχ. πάει στην τομή της εκ του

κάθετης στην

με την εκ του

κάθετη στην
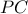
(και όμοια και για τα άλλα).Η ευθεία Simson (
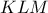
) πάει στον κύκλο

.
Εμείς θέλουμε να δείξουμε πως το κέντρο

του αρχικού

βρισκόταν πάνω στην ευθεία Simson
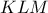
.
Ισοδύναμα,μετά την αντιστροφή αρκεί/πρέπει να δείξουμε πως οι

,

είναι ορθογώνιοι:Αν ισχύει αυτό,επειδή το

ανήκει στον

το αντίστροφό του προς τον

θα ανήκει επίσης στον
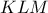
.Είναι σχετικά απλό πως αυτό το σημείο είναι το αντίστροφο του

ως προς την αρχική αντιστροφή κλπ.
Από δω και πέρα ασχολούμαστε μόνο με το αντίστροφο σχήμα:

- simsonasads1.png (107.43 KiB) Προβλήθηκε 1721 φορές
Έστω

το κέντρο του

(όχι το αντίστροφο του

αφού η αντιστροφή δε στέλνει κέντρο κύκλου στο κέντρο του αντίστροφού του) και

το κέντρο του

.Θέλουμε να δείξουμε πως η εφαπτόμενη του

στον

περνάει από σημείο τομής των δύο κύκλων.
Έχουμε όπως είπαμε πως

κάθετες (παραπάνω),

κάθετες (αντιδιαμετρικά σημεία) και

κάθετες(παραπάνω).Συνεπώς

κάθετες και με όμοιο συλλογισμό προκύπτει τελικά πως τα
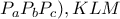
είναι όμοια τρίγωνα με κάθετες πλευρές.
Έστω

.
Τα

είναι αντιδιαμετρικά του

ως προς τους
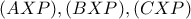
(απλό,παραπάνω καθετότητες).
Άρα από ομοιοθεσία λόγου 2 (λόγω του ότι οι
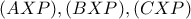
είμαι ομοαξονικοί/έχουν συνευθειακά κέντρα) είναι και συνευθειακά.
Απομονώνοντας λίγο το σχήμα,έχουμε τα προοπτικά/αντιστρόφως όμοια τρίγωνα με κάθετες πλευρές (παραπάνω καθετότητες) που τέμνονται στα

.(τα έβγαλα εκτός των τριγώνων για να φαίνονται καλύτερα).

- simsonasapom1.png (30.01 KiB) Προβλήθηκε 1721 φορές
Αν

ισχύει

από εγγράψιμα.Άρα
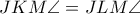
δηλαδή το

ανήκει στον

και ομοίως ανήκει και στον

.Τελικά από το

περνάει και η
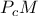
.
Αν το άλλο σημείο τομής των 2 κύκλων είναι το
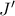
τότε από Σπειροειδή ομοιότητα (spiral similarity) ή τελοσπάντων κανονική ομοιότητα,το
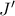
στέλνει με Σπειροειδή ομοιότητα το

στο

.(Ουσιαστικά σύνθεση στροφής/ομοιοθεσίας).Τα δύο τμήματα είναι κάθετα άρα η στροφή είναι κατά ορθή γωνία.Άρα
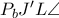
πχ. ορθή.Ο ίδιος μετασχηματισμός στέλνει τον αριστερό κύκλο στο δεξί,συνεπώς στέλνει το
κέντρο

στο κέντρο

.(από ομοιότητες).Άρα και η

είναι ορθή,πράγμα που σημαίνει πως οι 2 κύκλοι είναι ορθογώνιοι από όπου έπεται το ζητούμενο...
Σημ:Στην περίπτωση που το

πάει στο άπειρο,η αντιστροφή θα δημιουργήσει ομοαξονικούς κύκλους με 1 κοινό σημείο (ομοιόθετοι στο

).Η απόδειξη δεν αλλάζει σημαντικά.Παρ'όλα αυτά,γενικά θέλει λιγάκι προσοχή το πότε λειτουργούν επιχειρήματα του τύπου "στέλνω στο άπειρο",ιδίως από τη στιγμή που η παραπάνω λύση δεν είναι προβολική.
 και ευθεία
και ευθεία  του επιπέδου του. Έστω
του επιπέδου του. Έστω  τυχαίο σημείο του περικυκλίου του
τυχαίο σημείο του περικυκλίου του  , και
, και  τα σημεία τομής των
τα σημεία τομής των  προς την
προς την  με τις κάθετες στο σημείο
με τις κάθετες στο σημείο  επί των ευθειών
επί των ευθειών  αντίστοιχα.
αντίστοιχα.  είναι οι ορθές προβολές του
είναι οι ορθές προβολές του  επί των ευθειών των πλευρών
επί των ευθειών των πλευρών  του τριγώνου
του τριγώνου  αντίστοιχα,
αντίστοιχα,  του περίκυκλου του τριγώνου
του περίκυκλου του τριγώνου  ανήκει στην ευθεία
ανήκει στην ευθεία  του σημείου
του σημείου  ως προς το τρίγωνο
ως προς το τρίγωνο 

 και σημείο
και σημείο  του
του  .Έτσω τυχαίες σεβιανές του τριγώνου που συντρέχουν σε σημείο
.Έτσω τυχαίες σεβιανές του τριγώνου που συντρέχουν σε σημείο  .Ορίζουμε
.Ορίζουμε  την τομή της
την τομή της  με την εκ του
με την εκ του  .Ανάλογα ορίζονται και τα
.Ανάλογα ορίζονται και τα  .Έστω
.Έστω  ο ποδικός κύκλος ως προς το
ο ποδικός κύκλος ως προς το  .Τότε το κέντρο του κύκλου αυτού
.Τότε το κέντρο του κύκλου αυτού  βρίσκεται στην ευθεία Simson του
βρίσκεται στην ευθεία Simson του 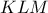 )
) πάνε σε ευθεία.
πάνε σε ευθεία.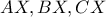 πάνε στους ομοαξονικούς κύκλους
πάνε στους ομοαξονικούς κύκλους 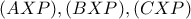 .
. πάνε στα αντιδιαμετρικά των
πάνε στα αντιδιαμετρικά των  είναι ομοκυκλικά,όπως και τα αντίστοιχά τους,(και λόγω του
είναι ομοκυκλικά,όπως και τα αντίστοιχά τους,(και λόγω του  κτλ.), το
κτλ.), το  πάει στην τομή της εκ του
πάει στην τομή της εκ του  κάθετης στην
κάθετης στην 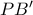 με την εκ του
με την εκ του  κάθετη στην
κάθετη στην 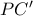 .(Όμοια και για τα άλλα).
.(Όμοια και για τα άλλα). κτλ. το
κτλ. το  πχ. πάει στην τομή της εκ του
πχ. πάει στην τομή της εκ του  κάθετης στην
κάθετης στην  με την εκ του
με την εκ του  κάθετη στην
κάθετη στην 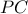 (και όμοια και για τα άλλα).Η ευθεία Simson (
(και όμοια και για τα άλλα).Η ευθεία Simson ( .
. βρισκόταν πάνω στην ευθεία Simson
βρισκόταν πάνω στην ευθεία Simson  είναι ορθογώνιοι:Αν ισχύει αυτό,επειδή το
είναι ορθογώνιοι:Αν ισχύει αυτό,επειδή το  το κέντρο του
το κέντρο του  το κέντρο του
το κέντρο του  .Θέλουμε να δείξουμε πως η εφαπτόμενη του
.Θέλουμε να δείξουμε πως η εφαπτόμενη του  κάθετες (παραπάνω),
κάθετες (παραπάνω), κάθετες (αντιδιαμετρικά σημεία) και
κάθετες (αντιδιαμετρικά σημεία) και  κάθετες(παραπάνω).Συνεπώς
κάθετες(παραπάνω).Συνεπώς  κάθετες και με όμοιο συλλογισμό προκύπτει τελικά πως τα
κάθετες και με όμοιο συλλογισμό προκύπτει τελικά πως τα 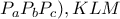 είναι όμοια τρίγωνα με κάθετες πλευρές.
είναι όμοια τρίγωνα με κάθετες πλευρές. .
. είναι αντιδιαμετρικά του
είναι αντιδιαμετρικά του  ισχύει
ισχύει  από εγγράψιμα.Άρα
από εγγράψιμα.Άρα 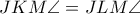 δηλαδή το
δηλαδή το  ανήκει στον
ανήκει στον 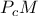 .
.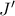 τότε από Σπειροειδή ομοιότητα (spiral similarity) ή τελοσπάντων κανονική ομοιότητα,το
τότε από Σπειροειδή ομοιότητα (spiral similarity) ή τελοσπάντων κανονική ομοιότητα,το  στο
στο  .(Ουσιαστικά σύνθεση στροφής/ομοιοθεσίας).Τα δύο τμήματα είναι κάθετα άρα η στροφή είναι κατά ορθή γωνία.Άρα
.(Ουσιαστικά σύνθεση στροφής/ομοιοθεσίας).Τα δύο τμήματα είναι κάθετα άρα η στροφή είναι κατά ορθή γωνία.Άρα 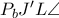 πχ. ορθή.Ο ίδιος μετασχηματισμός στέλνει τον αριστερό κύκλο στο δεξί,συνεπώς στέλνει το
πχ. ορθή.Ο ίδιος μετασχηματισμός στέλνει τον αριστερό κύκλο στο δεξί,συνεπώς στέλνει το είναι ορθή,πράγμα που σημαίνει πως οι 2 κύκλοι είναι ορθογώνιοι από όπου έπεται το ζητούμενο...
είναι ορθή,πράγμα που σημαίνει πως οι 2 κύκλοι είναι ορθογώνιοι από όπου έπεται το ζητούμενο...