Να πω εδώ ότι το συμπέρασμα εξακολουθεί να ισχύει αν το ορθόκεντρο αντικατασταθεί με οποιοδήποτε (εσωτερικό) σημείο του τριγώνου.Απόδειξη για αυτό δε βρήκα,αλλά βρήκα για οποιοδήποτε σημείο
εσωτερικό του εγγεγραμμένου κύκλου.
Αυτός ο περιορισμός έρχεται από την Προβολική Γεωμετρία:Το πρόβλημα είναι εξ'ολοκλήρου προβολικό.Για αυτό το λόγο παίρνουμε προβολικό μετασχηματισμό που στέλνει τον εγγεγραμμένο κύκλο στον εγγεγραμμένο του νέου τριγώνου και το σημείο

στο κέντρο του νέου κύκλου.Αυτό γίνεται μόνο όταν το

είναι εσωτερικό του κύκλου.Μια καταασκευή (την πήρα από τον

) του μετασχηματισμού είναι η ακόλουθη:Ουσιαστικά στέλνουμε την πολική του

ως προς τον κύκλο στην ευθεία στο άπειρο στέλνοντας παράλληλα τον κύκλο σε κύκλο.Τότε ο πόλος της ευθείας (το

) θα σταλεί στο κέντρο του κύκλου.Είναι απαραίτητο η πολική να μην τέμνει τον κύκλο (εξ'ού και ο περιορισμός).
Αν ισχύει αυτό,τότε παίρνουμε μια σφαίρα που να έχει στην περιφέρειά της τον κύκλο μας.Φέρνουμε έπειτα το εφαπτόμενο επίπεδο από την πολική στη σφαίρα και έστω ότι την αγγίζει στο  .Παίρνουμε το εφαπτόμενο επίπεδο στη σφαίρα στο αντιδιαμετρικό σημείο του
.Παίρνουμε το εφαπτόμενο επίπεδο στη σφαίρα στο αντιδιαμετρικό σημείο του  και προβάλλουμε από το
και προβάλλουμε από το  το αρχικό μας επίπεδο στο εφαπτόμενο.Η πολική,λόγω παραλληλίας με το επίπεδο,πάει στο άπειρο,ενώ ο κύκλος,από ιδιότητες της στερεογραφικής απεικόνισης πηγαίνει σε κύκλο..
το αρχικό μας επίπεδο στο εφαπτόμενο.Η πολική,λόγω παραλληλίας με το επίπεδο,πάει στο άπειρο,ενώ ο κύκλος,από ιδιότητες της στερεογραφικής απεικόνισης πηγαίνει σε κύκλο..

- ths nixtas ta kamwmata.png (76.86 KiB) Προβλήθηκε 2730 φορές
Άρα όντως μπορούμε να στείλουμε το

στο κέντρο του (νέου) εγγεγραμμένου με κατάλληλο προβολικό μετασχηματισμό (μην ξεχνάμε πως οι προβολικοί μετασχηματισμοί διατηρούν τομές/εφάψεις).Άρα αρκεί να δειχτεί το ανάλογο του αρχικού για το κέντρο του εγγεγραμμένου

.
Στο σχήμα είναι

,

αντίστοιχα και τα υπόλοιπα αντίστοιχα (όπως φαίνεται..).Αρκεί (όπως και στο αρχικό πρόβλημα) να δειχτεί πως τα

είναι προοπτικά.
Αν φέρουμε την εφαπτομένη στο

και

τα σημεία που τέμνει τις

αντίστοιχα,τότε

από ιδιότητες αρμονικού τετραπλεύρου.'Αρα οι 2 αυτές σημειοσειρές είναι προοπτικές πράγμα που σημαίνει πως οι

συντρέχουν,και επειδή οι 2 τελευταίες τέμνονται στο άπειρο της

,θα είναι και η

παράλληλη με αυτές.Άρα

.Αν

και αντίστοιχα οριστούν τα

(ως προς τις B,C αντίστοιχα) τότε ισχύει πως η πολική του

ως προς τον εγγεγραμμένο είναι η

και αντίστοιχα και για τα

.(Η πολική του

είναι η

και του

η

κλπ.).Έτσι,η

είναι η πολική του

,

είναι η πολική του

και

είναι η πολική του

.Εμείς θέμε τα

,

,

να βγουν συνευθειακά.Συνεπώς,ισοδύναμα από τις πολικότητες αρκεί οι

να συντρέχουν.Αυτό το δείχνουμε μετρικά (έχει κάπως άχαρες πράξεις,αλλά τίποτα το ιδιαίτερο).
Αρχίζουμε:
Από Τριγωνομετρικό Ceva στο

με συντρέχουσες τις

παίρνουμε

.Εμείς θέμε

δηλαδή πολλαπλασιάζοντας τα αντίστοιχα

της

να βγαίνει γινόμενο

.
Έστω

.Το

της

γίνεται από παραλληλίες/νόμους ημιτόνων κλπ. ίσο με

.

- ths nixtas'.png (90.86 KiB) Προβλήθηκε 2730 φορές
Ορίζουμε τα

πάνω στην εφαπτομένη στο

όπως ορίστηκαν τα

, και τα

στην

όπως τα

.Το ίδιο κάνουμε και για τα

(στην εφ. στο

) και

(στην

) .
Τότε τα

των αντίστοιχων της

για αυτά τα σημεία (το γινόμενο των οποίων θέμε να βγει

) είναι

.
Αρκεί

το οποίο από Θαλήδες απλοποιείται στο

.Στη συνέχεια υπολογίζουμε κάθε τμήμα ξεχωριστά (αρκεί ο υπολογισμός να γίνει για το

πχ. λόγω συμμετρίας/κυκλικότητας.
Έστω

,

το μέσο της

.Ισχύουν:

(ομοιότητες) (3)
Από (3)
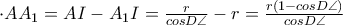
(4)
Από (4)

(5)
Από (5)

(Θαλής,

)(

) (6)
Από (6)

(7)
Από νόμο Ημιτόνων/παραλληλίες/την (7)

(8)

(9)
Από Θαλή,(7),(8),(9):

(

οι αντίστοιχες πλευρές του εγγεγραμμένου τριγώνου)
Η παραπάνω απλοποιείται περαιτέρω σε
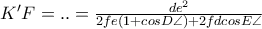
.
Ομοίως παίρνουμε και





Αν στις παραπάνω 6 σχέσεις συμβολίσουμε με

τον παρονομαστή της αντίστοιχης σχέσης,η

που θέμε να δείξουμε (επειδή φεύγουν οι αριθμητές) μετατρέπεται σε

που έπειτα από απλοποιήσεις δίνει την
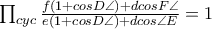
Από εδώ τα πράγματα είναι απλά.Αν φέρουμε τα κατάλληλα ύψη βλέπουμε πως

.Έτσι η τελευταία γίνεται

και το ζητούμενο δείχτηκε.
 και ο εγγεγραμμένος του κύκλος
και ο εγγεγραμμένος του κύκλος  . Ας είναι
. Ας είναι  τα σημεία επαφής του
τα σημεία επαφής του  με τις πλευρές
με τις πλευρές  αντίστοιχα.
αντίστοιχα.  τα ύψη του
τα ύψη του  και
και  τα σημεία τομής των
τα σημεία τομής των  με τον
με τον  τα πλησιέστερα των κορυφών
τα πλησιέστερα των κορυφών  αντίστοιχα.
αντίστοιχα.
 και
και  να δειχθεί ότι οι ευθείες
να δειχθεί ότι οι ευθείες  διέρχονται από το ίδιο σημείο ( έστω
διέρχονται από το ίδιο σημείο ( έστω  ).
).
 στο κέντρο του νέου κύκλου.Αυτό γίνεται μόνο όταν το
στο κέντρο του νέου κύκλου.Αυτό γίνεται μόνο όταν το  ) του μετασχηματισμού είναι η ακόλουθη:Ουσιαστικά στέλνουμε την πολική του
) του μετασχηματισμού είναι η ακόλουθη:Ουσιαστικά στέλνουμε την πολική του  .Παίρνουμε το εφαπτόμενο επίπεδο στη σφαίρα στο αντιδιαμετρικό σημείο του
.Παίρνουμε το εφαπτόμενο επίπεδο στη σφαίρα στο αντιδιαμετρικό σημείο του  .
. ,
, αντίστοιχα και τα υπόλοιπα αντίστοιχα (όπως φαίνεται..).Αρκεί (όπως και στο αρχικό πρόβλημα) να δειχτεί πως τα
αντίστοιχα και τα υπόλοιπα αντίστοιχα (όπως φαίνεται..).Αρκεί (όπως και στο αρχικό πρόβλημα) να δειχτεί πως τα  είναι προοπτικά.
είναι προοπτικά. και
και  τα σημεία που τέμνει τις
τα σημεία που τέμνει τις  αντίστοιχα,τότε
αντίστοιχα,τότε  από ιδιότητες αρμονικού τετραπλεύρου.'Αρα οι 2 αυτές σημειοσειρές είναι προοπτικές πράγμα που σημαίνει πως οι
από ιδιότητες αρμονικού τετραπλεύρου.'Αρα οι 2 αυτές σημειοσειρές είναι προοπτικές πράγμα που σημαίνει πως οι  συντρέχουν,και επειδή οι 2 τελευταίες τέμνονται στο άπειρο της
συντρέχουν,και επειδή οι 2 τελευταίες τέμνονται στο άπειρο της  ,θα είναι και η
,θα είναι και η  παράλληλη με αυτές.Άρα
παράλληλη με αυτές.Άρα  .Αν
.Αν  και αντίστοιχα οριστούν τα
και αντίστοιχα οριστούν τα  (ως προς τις B,C αντίστοιχα) τότε ισχύει πως η πολική του
(ως προς τις B,C αντίστοιχα) τότε ισχύει πως η πολική του  ως προς τον εγγεγραμμένο είναι η
ως προς τον εγγεγραμμένο είναι η 
 και του
και του 
 κλπ.).Έτσι,η
κλπ.).Έτσι,η  είναι η πολική του
είναι η πολική του 
 είναι η πολική του
είναι η πολική του 
 είναι η πολική του
είναι η πολική του 
 ,
, ,
, να βγουν συνευθειακά.Συνεπώς,ισοδύναμα από τις πολικότητες αρκεί οι
να βγουν συνευθειακά.Συνεπώς,ισοδύναμα από τις πολικότητες αρκεί οι  να συντρέχουν.Αυτό το δείχνουμε μετρικά (έχει κάπως άχαρες πράξεις,αλλά τίποτα το ιδιαίτερο).
να συντρέχουν.Αυτό το δείχνουμε μετρικά (έχει κάπως άχαρες πράξεις,αλλά τίποτα το ιδιαίτερο). με συντρέχουσες τις
με συντρέχουσες τις  παίρνουμε
παίρνουμε  .Εμείς θέμε
.Εμείς θέμε  δηλαδή πολλαπλασιάζοντας τα αντίστοιχα
δηλαδή πολλαπλασιάζοντας τα αντίστοιχα  της
της  να βγαίνει γινόμενο
να βγαίνει γινόμενο  .
. .Το
.Το  .
.
 πάνω στην εφαπτομένη στο
πάνω στην εφαπτομένη στο  όπως ορίστηκαν τα
όπως ορίστηκαν τα 
 όπως τα
όπως τα 
 (στην εφ. στο
(στην εφ. στο  ) και
) και 
 ) .
) . .
. το οποίο από Θαλήδες απλοποιείται στο
το οποίο από Θαλήδες απλοποιείται στο  .Στη συνέχεια υπολογίζουμε κάθε τμήμα ξεχωριστά (αρκεί ο υπολογισμός να γίνει για το
.Στη συνέχεια υπολογίζουμε κάθε τμήμα ξεχωριστά (αρκεί ο υπολογισμός να γίνει για το  πχ. λόγω συμμετρίας/κυκλικότητας.
πχ. λόγω συμμετρίας/κυκλικότητας. ,
, το μέσο της
το μέσο της  (ομοιότητες) (3)
(ομοιότητες) (3)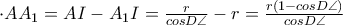 (4)
(4) (5)
(5) (Θαλής,
(Θαλής, )(
)( ) (6)
) (6) (7)
(7) (8)
(8) (9)
(9) (
( οι αντίστοιχες πλευρές του εγγεγραμμένου τριγώνου)
οι αντίστοιχες πλευρές του εγγεγραμμένου τριγώνου)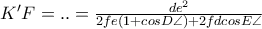 .
.




 τον παρονομαστή της αντίστοιχης σχέσης,η
τον παρονομαστή της αντίστοιχης σχέσης,η  που θέμε να δείξουμε (επειδή φεύγουν οι αριθμητές) μετατρέπεται σε
που θέμε να δείξουμε (επειδή φεύγουν οι αριθμητές) μετατρέπεται σε  που έπειτα από απλοποιήσεις δίνει την
που έπειτα από απλοποιήσεις δίνει την 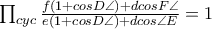
 .Έτσι η τελευταία γίνεται
.Έτσι η τελευταία γίνεται  και το ζητούμενο δείχτηκε.
και το ζητούμενο δείχτηκε. ).
). .
. και
και  είναι προοπτικά:
είναι προοπτικά: τις τομές των
τις τομές των 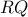 και
και  ,
, 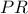 και
και  ,
,  και
και  αντίστοιχα, τότε από
αντίστοιχα, τότε από  αρκεί τα
αρκεί τα  και ας επικεντρωθούμε στο
και ας επικεντρωθούμε στο 
 .
.
 (1) (μπορεί να έβγαινε και πιο απλά αλλά τέλος πάντων)
(1) (μπορεί να έβγαινε και πιο απλά αλλά τέλος πάντων) (2)
(2) (3)
(3) .
. , άρα αρκεί:
, άρα αρκεί: (*).
(*). .
. τέμνει την
τέμνει την  στο
στο  . Αφού η
. Αφού η  .
. και
και  , προκύπτει ότι
, προκύπτει ότι  , οπότε τελικά:
, οπότε τελικά:
 , που ισχύει από Ceva για τις αρχικές σεβιανές!
, που ισχύει από Ceva για τις αρχικές σεβιανές! σημεία στο επίπεδο.
σημεία στο επίπεδο. τα κυκλοσεβιανά των
τα κυκλοσεβιανά των  το τρίγωνο που ορίζεται από τις
το τρίγωνο που ορίζεται από τις  .
. και
και  τα αντίστοιχά του σημεία.
τα αντίστοιχά του σημεία. .
. παίρνουμε την αρχική γενίκευση.
παίρνουμε την αρχική γενίκευση. ,και
,και  τα κυκλικά του,αρκεί
τα κυκλικά του,αρκεί  .
.
 .
. και από
και από  (
( )
)
 και τα κυκλικά του..
και τα κυκλικά του.. είναι προοπτικά.
είναι προοπτικά. και τις κυκλικές τους.
και τις κυκλικές τους. είναι το τυχαίο
είναι το τυχαίο  συντρέχουν σε σημείο
συντρέχουν σε σημείο  (εντός του τριγώνου
(εντός του τριγώνου  και επανορίζω τα
και επανορίζω τα  ως τις τομές των
ως τις τομές των  με τον
με τον  και το
και το  .
. τότε προφανώς το αντίστοιχο
τότε προφανώς το αντίστοιχο  ,όπου
,όπου  πολυώνυμα ως προς την παράμετρο
πολυώνυμα ως προς την παράμετρο  ,το
,το  .(Ομοίως-δυικά ορίζεται και ο βαθμός κίνησης της ευθείας).
.(Ομοίως-δυικά ορίζεται και ο βαθμός κίνησης της ευθείας). οι βαθμοί των σημείων
οι βαθμοί των σημείων  ,τότε ο βαθμός της ευθείας
,τότε ο βαθμός της ευθείας  είναι το πολύ
είναι το πολύ  .
. τότε η εξίσωση της
τότε η εξίσωση της  από όπου οι βαθμοί των συντελεστών είναι πράγματι το πολύ
από όπου οι βαθμοί των συντελεστών είναι πράγματι το πολύ  ,σε κωνική δε).
,σε κωνική δε). έχουν βαθμό το πολύ
έχουν βαθμό το πολύ  (
( έχουν βαθμό
έχουν βαθμό  ).
). λοιπόν έχουν βαθμό το πολύ
λοιπόν έχουν βαθμό το πολύ  ως τομές σταθερών και δευτεροβάθμιων ευθειών (
ως τομές σταθερών και δευτεροβάθμιων ευθειών ( έχουν βαθμό
έχουν βαθμό  .Παρομοίως,
.Παρομοίως, .
. (από το λήμμα) και άρα αν
(από το λήμμα) και άρα αν  τα
τα  θα έχουν βαθμό το πολύ
θα έχουν βαθμό το πολύ  .
. τιμές της παραμέτρου
τιμές της παραμέτρου