 και
και  του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου  τέμνονται στο
τέμνονται στο  .
.Η κάθετη από το
 προς την υποτείνουσα , την τέμνει στο
προς την υποτείνουσα , την τέμνει στο  και την
και την  στο
στο  .
.Υπολογίστε τα μήκη των τμημάτων
 και
και  .
.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 και
και  του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου  τέμνονται στο
τέμνονται στο  .
. προς την υποτείνουσα , την τέμνει στο
προς την υποτείνουσα , την τέμνει στο  και την
και την  στο
στο  .
. και
και  .
.Εξαιτίας των πολλών υπολογισμών θα παραλείψω τους πιο προφανείς. Φέρνω τηνKARKAR έγραψε:Σληροϋπολογιστική.pngΟι διχοτόμοικαι
του ορθογωνίου τριγώνου
τέμνονται στο
.
Η κάθετη από τοπρος την υποτείνουσα , την τέμνει στο
και την
στο
.
Υπολογίστε τα μήκη των τμημάτωνκαι
.
 που τέμνει την
που τέμνει την  στο
στο  . Από Πυθαγόρειο θεώρημα, θεωρήματα διχοτόμων και τις σχέσεις
. Από Πυθαγόρειο θεώρημα, θεωρήματα διχοτόμων και τις σχέσεις 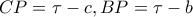 ,
,  , προκύπτουν οι τιμές των τμημάτων στο σχήμα. Είναι
, προκύπτουν οι τιμές των τμημάτων στο σχήμα. Είναι  κι επειδή
κι επειδή  , το
, το  είναι μέσο του
είναι μέσο του 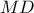 . Αλλά,
. Αλλά,  , άρα το
, άρα το  είναι μέσο του
είναι μέσο του  . Επομένως
. Επομένως 
 ,
,  . Άρα:
. Άρα: 
 έχουμε :
έχουμε :  και
και  .
. διχοτόμος της γωνίας
διχοτόμος της γωνίας  τότε
τότε  .
. διχοτόμος της γωνίας
διχοτόμος της γωνίας  τότε
τότε  .
. . (1)
. (1) . (2)
. (2)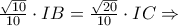
 .
. έχουμε :
έχουμε :













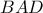



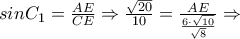
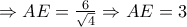


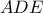


 Επειδή το τρίγωνο που ορίζεται από τις ευθείες δύο πλευρών τριγώνου και μια παράλληλη προς την τρίτη πλευρά του, έχει πλευρές ανάλογες προς τις πλευρές του αρχικού τριγώνου τότε:
Επειδή το τρίγωνο που ορίζεται από τις ευθείες δύο πλευρών τριγώνου και μια παράλληλη προς την τρίτη πλευρά του, έχει πλευρές ανάλογες προς τις πλευρές του αρχικού τριγώνου τότε: 



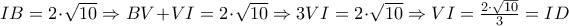
 μέσο του
μέσο του  .
. 
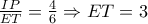

 και
και  προέκταση της
προέκταση της  τότε
τότε 


 έχουμε ότι
έχουμε ότι 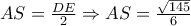
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης