Δίνουμε μια λύση:
Δυο καμπύλες Bertrand στον χώρο

,

, έχουν την ιδιότητα, για κάθε

, οι αντίστοιχες πρώτες κάθετες να ταυτίζονται.
[attachment=0]bertrand_curves.png[/attachment]
(i) η εξίσωση της πρώτης καθέτου της

στο σημείο

είναι

και η εξίσωση της πρώτης καθέτου της

στο σημείο

είναι

. Επειδή ταυτίζονται, ισχύουν
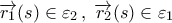
,

και

Δηλαδή η απόσταση μεταξύ των σημείων

και

είναι σταθερή.
(ii) Για τα αντίστοιχα μοναδιαία εφαπτόμενα των δύο καμπυλών ισχύει

Άρα η γωνία μεταξύ των αντίστοιχων εφαπτομένων των δυο καμπυλών είναι σταθερή.
 , ονομάζονται καμπύλες Bertrand, αν για κάθε
, ονομάζονται καμπύλες Bertrand, αν για κάθε  , οι αντίστοιχες πρώτες κάθετες ταυτίζονται. Δείξτε ότι, για κάθε
, οι αντίστοιχες πρώτες κάθετες ταυτίζονται. Δείξτε ότι, για κάθε  ,
, και
και  είναι σταθερή.
είναι σταθερή.

 ,
,  , έχουν την ιδιότητα, για κάθε
, έχουν την ιδιότητα, για κάθε  στο σημείο
στο σημείο  και η εξίσωση της πρώτης καθέτου της
και η εξίσωση της πρώτης καθέτου της  στο σημείο
στο σημείο  . Επειδή ταυτίζονται, ισχύουν
. Επειδή ταυτίζονται, ισχύουν 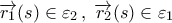 ,
,  και
και 
